Page 316 - Pressure Swing Adsorption

11
292 PRESSURE SWING ADSORPTION MEMBRANE PROCESSES
293
often compensation between the kinetic and eouilibnum parameters so that s
ores ure m a system in which the total bressure, on each side of the
the resulting separation factor 1s smaller than would be predicted by consid-
membrane, ts essentially constant but the cornoosition vanes with position.
ering either the diffus1v1ty rat10 or the equilibnum rat10 alone. This 1s
illustrated in Table 8.1.
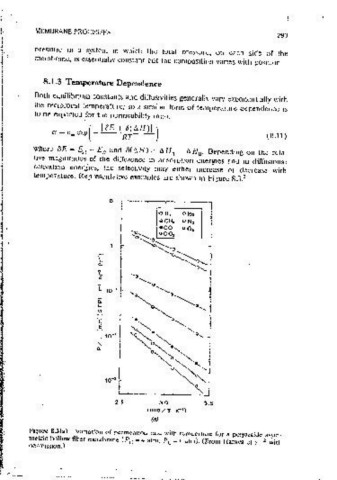
8.1.3 Temperature Dependence
8. 1. 1 Nonlinear Equilibrium Both eauilibnum constants anct diffus1vities generally varv exponentiallv with
the rec1orocal temperature; so a simiiar form of temperature deoencte~ce 15
Whether the equilibrium is linear or nonlinear, the expressmn for the flux to be expected for the Permeability ratio.
may be written m the form:
- ( [oE+o(AH)])·
dµ,A a - a~exp - RT (8.11)
NA - -LAqA dz (8.6)
where SE~ E - E anct o(AH) - AH A - u n· · epenctmg on the rela-
··
'H D
- u
where µ,A=µ,~+ RT In PA, with sunilar expressions for component B. The A B
tive m~gmtuctes of the difference in adsorption energies and in diffus10nal
flux ratio is given by: i activation energies, the selectivity may either increase or decrease. with
NA LA qA dµ,A DoA qA PB dpA I temperature. Representative examples are shown m Figure 8.3. z
- . (8~
N,J La Qa dµ,B Don qn PA dpR i
where D A = RTLA 1s the limiting diffusivity within the Henry's Law region.
0 j'
Ifthe eauilibnum isotherm 1s of binary Langmmr form (Eu. 2.13):
qApll bA I .
(8.8)
QnPA = bs
!
so that Ea. 8.7 reduces to:
NA DoA bA dpA dpA
(8.9)
NB ~ Dos bs dps = a dps
where a IS defined by Eo. 8.5. Integrating across the membrane yields Ea.
8.3, which is thus seen to be applicable even outside the Henry's Law region.
It should be noted that this s1mplificat10n arises only m the special case of an
ideal Langmuir system. For other forms of isothenn Eq. 8.5 is not necessarily
valid outside the linear regLOn.

8.1.2 Effect of Back Pressure
To auantify the effect of back pressure on the separation factor we may
elimmate y between Eas. 8.2 and 8.3. With -rrA/-rr = a (Ea. 8.4) this yields
8
1
the Naylor-Backer express1on •
a'~ ( 1: a) - z1x - a2~; (8.10)
2.5 3.0
. 27 l/2 3,S
2 1
+ [(" - 1 )' + r(a - 1) - (a - 1) _,_/a-l+r) 1 1000/Tf K- 1
2 2ffJx - \ 2ffJx . l {a)
In the high-pressure limit (P -4> oo) this reduces simply to a' = a. Eauat1on ::~~ :~~~) firanatfon bof pe(;eatmn rate with temoerture for a polyamide asvm-
8.10 provides ttle most convenient way to account for the effect of bacK penmss10n.) w er mem rane H = 4 atm, p L = I atm). (From Hara ya et al., 2 with