Page 197 -

6.4 Region-Based Mining 179

2
3
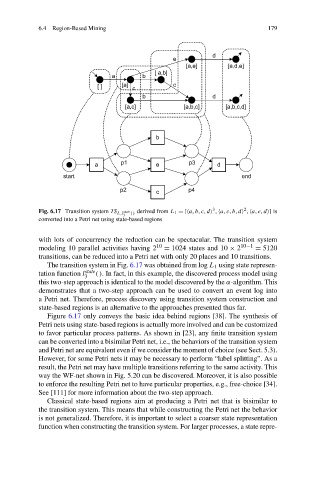
Fig. 6.17 Transition system TS L,l 3 state () derived from L 1 =[ a,b,c,d , a,c,b,d , a,e,d ] is
converted into a Petri net using state-based regions
with lots of concurrency the reduction can be spectacular. The transition system
modeling 10 parallel activities having 2 10 = 1024 states and 10 × 2 10−1 = 5120
transitions, can be reduced into a Petri net with only 20 places and 10 transitions.
The transition system in Fig. 6.17 was obtained from log L 1 using state represen-
tation function l state (). In fact, in this example, the discovered process model using
3
this two-step approach is identical to the model discovered by the α-algorithm. This
demonstrates that a two-step approach can be used to convert an event log into
a Petri net. Therefore, process discovery using transition system construction and
state-based regions is an alternative to the approaches presented thus far.
Figure 6.17 only conveys the basic idea behind regions [38]. The synthesis of
Petri nets using state-based regions is actually more involved and can be customized
to favor particular process patterns. As shown in [23], any finite transition system
can be converted into a bisimilar Petri net, i.e., the behaviors of the transition system
and Petri net are equivalent even if we consider the moment of choice (see Sect. 5.3).
However, for some Petri nets it may be necessary to perform “label splitting”. As a
result, the Petri net may have multiple transitions referring to the same activity. This
way the WF-net shown in Fig. 5.20 can be discovered. Moreover, it is also possible
to enforce the resulting Petri net to have particular properties, e.g., free-choice [34].
See [111] for more information about the two-step approach.
Classical state-based regions aim at producing a Petri net that is bisimilar to
the transition system. This means that while constructing the Petri net the behavior
is not generalized. Therefore, it is important to select a coarser state representation
function when constructing the transition system. For larger processes, a state repre-