Page 122 - Reliability and Maintainability of In service Pipelines

Time-Dependent Reliability Analysis 111

given, f x ðx 1 ; x 2 ; ... ; x n ; θÞ is a function of θ alone, and the value of θ that maxi-
mizes the above probability density function is the most likely value for θ.
In the current study a typical data set consists of inspection times
t i ; i 5 1; ... ; n where 0 5 t 0 , t 1 , t 2 , ... , t n , and corresponding observations
of the cumulative amounts of deterioration d i; i 5 1; ... ; n are assumed to be given
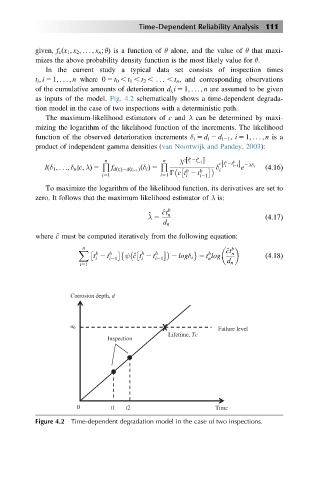
as inputs of the model. Fig. 4.2 schematically shows a time-dependent degrada-
tion model in the case of two inspections with a deterministic path.
The maximum-likelihood estimators of c and λ can be determined by maxi-
mizing the logarithm of the likelihood function of the increments. The likelihood
function of the observed deterioration increments δ i 5 d i 2 d i21 , i 5 1; ... ; n is a
product of independent gamma densities (van Noortwijk and Pandey, 2003):
b
b
n n λ ct 2t Š b b
i ½
i21
i ½
i21
e
j ðÞ δ ct 2t Š 2λδ i ð4:16Þ
lðδ 1 ; ...; δ n c; λÞ 5 L f dt i ðÞ2dt i21 Þ δ i 5 L i
ð b b
i
i51 i51 Γ ct 2 t i21
To maximize the logarithm of the likelihood function, its derivatives are set to
zero. It follows that the maximum likelihood estimator of λ is:
^
λ 5 ^ ct b n ð4:17Þ
d n
where ^ c must be computed iteratively from the following equation:
n ^ ct b

b
X
b

b

t 2 t b ψ ^ ct 2 t b 2 logδ i 5 t log n ð4:18Þ
i i21 i i21 n
d n
i51
Corrosion depth, d
a 0
Failure level
Lifetime, Tc
Inspection

0 t1 t2 Time

Figure 4.2 Time-dependent degradation model in the case of two inspections.