Page 177 - Rock Mechanics For Underground Mining

RESULTS OF IN SITU STRESS MEASUREMENTS

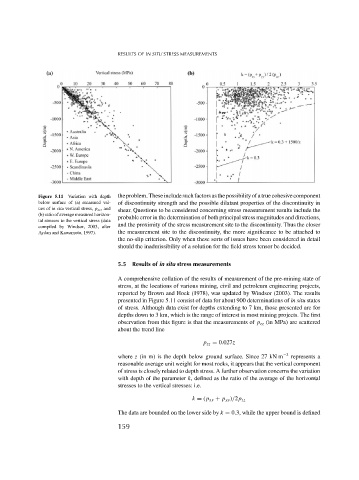
Figure 5.11 Variation with depth the problem. These include such factors as the possibility of a true cohesive component
below surface of (a) measured val- of discontinuity strength and the possible dilatant properties of the discontinuity in
ues of in situ vertical stress, p zz , and
shear. Questions to be considered concerning stress measurement results include the
(b) ratio of average measured horizon-
probable error in the determination of both principal stress magnitudes and directions,
tal stresses to the vertical stress (data
and the proximity of the stress measurement site to the discontinuity. Thus the closer
compiled by Windsor, 2003, after
Aydan and Kawamoto, 1997). the measurement site to the discontinuity, the more significance to be attached to
the no-slip criterion. Only when these sorts of issues have been considered in detail
should the inadmissibility of a solution for the field stress tensor be decided.
5.5 Results of in situ stress measurements

A comprehensive collation of the results of measurement of the pre-mining state of
stress, at the locations of various mining, civil and petroleum engineering projects,
reported by Brown and Hoek (1978), was updated by Windsor (2003). The results
presented in Figure 5.11 consist of data for about 900 determinations of in situ states
of stress. Although data exist for depths extending to 7 km, those presented are for
depths down to 3 km, which is the range of interest in most mining projects. The first
observation from this figure is that the measurements of p zz (in MPa) are scattered
about the trend line
p zz = 0.027z

where z (in m) is the depth below ground surface. Since 27 kN m −3 represents a
reasonable average unit weight for most rocks, it appears that the vertical component
of stress is closely related to depth stress. A further observation concerns the variation
with depth of the parameter k, defined as the ratio of the average of the horizontal
stresses to the vertical stresses: i.e.

k = (p xx + p yy )/2p zz

The data are bounded on the lower side by k = 0.3, while the upper bound is defined
159