Page 294 - Rock Mechanics For Underground Mining

ENERGY, MINE STABILITY, MINE SEISMICITY AND ROCKBURSTS

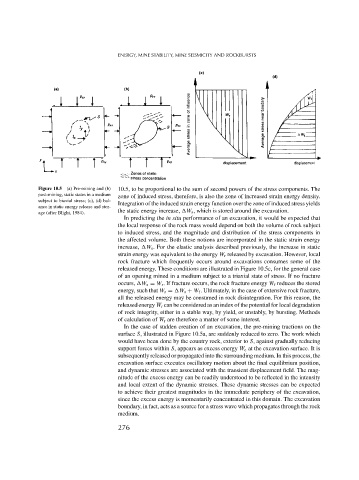
Figure 10.5 (a) Pre-mining and (b) 10.5, to be proportional to the sum of second powers of the stress components. The
post-mining, static states in a medium zone of induced stress, therefore, is also the zone of increased strain energy density.
subject to biaxial stress; (c), (d) bal-
Integration of the induced strain energy function over the zone of induced stress yields
ance in static energy release and stor-
the static energy increase, W s , which is stored around the excavation.
age (after Blight, 1984).
In predicting the in situ performance of an excavation, it would be expected that
the local response of the rock mass would depend on both the volume of rock subject
to induced stress, and the magnitude and distribution of the stress components in
the affected volume. Both these notions are incorporated in the static strain energy
increase, W s . For the elastic analysis described previously, the increase in static
strain energy was equivalent to the energy W r released by excavation. However, local
rock fracture which frequently occurs around excavations consumes some of the
released energy. These conditions are illustrated in Figure 10.5c, for the general case
of an opening mined in a medium subject to a triaxial state of stress. If no fracture
occurs, W s = W r . If fracture occurs, the rock fracture energy W f reduces the stored
energy, such that W r = W s + W f . Ultimately, in the case of extensive rock fracture,
all the released energy may be consumed in rock disintegration. For this reason, the
released energy W r can be considered as an index of the potential for local degradation
of rock integrity, either in a stable way, by yield, or unstably, by bursting. Methods
of calculation of W r are therefore a matter of some interest.
In the case of sudden creation of an excavation, the pre-mining tractions on the
surface S, illustrated in Figure 10.5a, are suddenly reduced to zero. The work which
would have been done by the country rock, exterior to S, against gradually reducing
support forces within S, appears as excess energy W e at the excavation surface. It is
subsequently released or propagated into the surrounding medium. In this process, the
excavation surface executes oscillatory motion about the final equilibrium position,
and dynamic stresses are associated with the transient displacement field. The mag-
nitude of the excess energy can be readily understood to be reflected in the intensity
and local extent of the dynamic stresses. These dynamic stresses can be expected
to achieve their greatest magnitudes in the immediate periphery of the excavation,
since the excess energy is momentarily concentrated in this domain. The excavation
boundary, in fact, acts as a source for a stress wave which propagates through the rock
medium.

276