Page 529 - Rock Mechanics For Underground Mining

CONTINUOUS SUBSIDENCE DUE TO THE MINING OF TABULAR OREBODIES

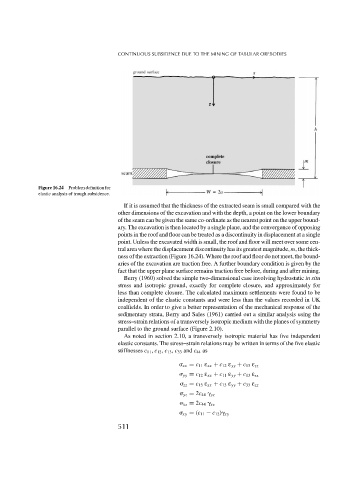
Figure 16.24 Problem definition for
elastic analysis of trough subsidence.
If it is assumed that the thickness of the extracted seam is small compared with the
other dimensions of the excavation and with the depth, a point on the lower boundary
of the seam can be given the same co-ordinate as the nearest point on the upper bound-
ary. The excavation is then located by a single plane, and the convergence of opposing
points in the roof and floor can be treated as a discontinuity in displacement at a single
point. Unless the excavated width is small, the roof and floor will meet over some cen-
tral area where the displacement discontinuity has its greatest magnitude, m, the thick-
ness of the extraction (Figure 16.24). Where the roof and floor do not meet, the bound-
aries of the excavation are traction free. A further boundary condition is given by the
fact that the upper plane surface remains traction free before, during and after mining.
Berry (1960) solved the simple two-dimensional case involving hydrostatic in situ
stress and isotropic ground, exactly for complete closure, and approximately for
less than complete closure. The calculated maximum settlements were found to be
independent of the elastic constants and were less than the values recorded in UK
coalfields. In order to give a better representation of the mechanical response of the
sedimentary strata, Berry and Sales (1961) carried out a similar analysis using the
stress–strain relations of a transversely isotropic medium with the planes of symmetry
parallel to the ground surface (Figure 2.10).
As noted in section 2.10, a transversely isotropic material has five independent
elastic constants. The stress–strain relations may be written in terms of the five elastic
stiffnesses c 11 , c 12 , c 13 , c 33 and c 44 as

xx = c 11 ε xx + c 12 ε yy + c 13 ε zz
yy = c 12 ε xx + c 11 ε yy + c 13 ε zz
zz = c 13 ε xx + c 13 ε yy + c 33 ε zz
yz = 2c 44 yz
xz = 2c 44 xz
xy = (c 11 − c 12 ) xy
511