Page 329 - Schaum's Outline of Theory and Problems of Applied Physics

314 CAPACITANCE [CHAP. 26

The formula that governs the growth of charge in the circuit of Fig. 26-6 is
Q = Q 0 (1 − e −t/T )

where Q 0 is the final charge CV and T is the time constant RC. Figure 26-7 is a graph of this formula. The
quantity e has the value

e = 2.718 ···
and is often found in equations in engineering and science. A quantity that consists of e raised to a power is
x
called an exponential. To find the value of e or e −x , an electronic calculator or a suitable table can be used.
x
Exponentials are sometimes written exp x or exp(−x) instead of e or e −x . The meaning is exactly the same.
It is easy to see why Q reaches 63 percent of Q 0 in time T. When t = T, t/T = 1 and

1
−1
Q = Q 0 (1 − e ) = Q 0 1 − = Q 0 (1 − 0.37) = 0.63Q 0
e
DISCHARGING A CAPACITOR
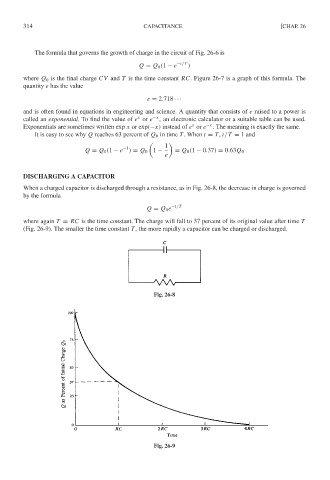
When a charged capacitor is discharged through a resistance, as in Fig. 26-8, the decrease in charge is governed
by the formula
−t/T
Q = Q 0 e
where again T = RC is the time constant. The charge will fall to 37 percent of its original value after time T
(Fig. 26-9). The smaller the time constant T, the more rapidly a capacitor can be charged or discharged.

Fig. 26-8

Fig. 26-9