Page 34 - Schaum's Outline of Theory and Problems of Applied Physics

CHAP. 2] VECTORS 19

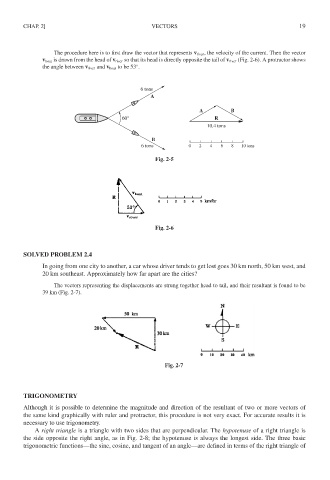
The procedure here is to first draw the vector that represents v river , the velocity of the current. Then the vector
v boat is drawn from the head of v river so that its head is directly opposite the tail of v river (Fig. 2-6). A protractor shows
the angle between v river and v boat to be 53 .
◦

6 tons
A

A B
60° R
10.4 tons

B
6 tons 0 2 4 6 8 10 tons

Fig. 2-5

Fig. 2-6

SOLVED PROBLEM 2.4

In going from one city to another, a car whose driver tends to get lost goes 30 km north, 50 km west, and
20 km southeast. Approximately how far apart are the cities?
The vectors representing the displacements are strung together head to tail, and their resultant is found to be
39 km (Fig. 2-7).

Fig. 2-7

TRIGONOMETRY
Although it is possible to determine the magnitude and direction of the resultant of two or more vectors of
the same kind graphically with ruler and protractor, this procedure is not very exact. For accurate results it is
necessary to use trigonometry.
A right triangle is a triangle with two sides that are perpendicular. The hypotenuse of a right triangle is
the side opposite the right angle, as in Fig. 2-8; the hypotenuse is always the longest side. The three basic
trigonometric functions—the sine, cosine, and tangent of an angle—are defined in terms of the right triangle of