Page 35 - Schaum's Outline of Theory and Problems of Applied Physics

20 VECTORS [CHAP. 2

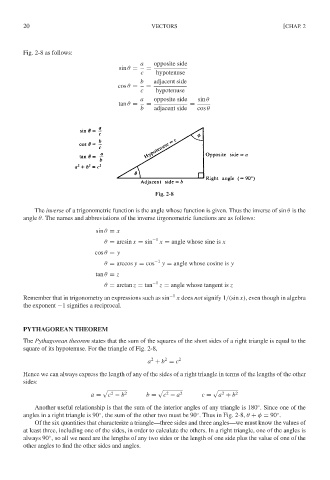
Fig. 2-8 as follows:
a opposite side
sin θ = =
c hypotenuse
b adjacent side
cos θ = =
c hypotenuse
a opposite side sin θ
tan θ = = =
b adjacent side cos θ

Fig. 2-8

The inverse of a trigonometric function is the angle whose function is given. Thus the inverse of sin θ is the
angle θ. The names and abbreviations of the inverse tirgonometric functions are as follows:

sin θ = x
θ = arcsin x = sin −1 x = angle whose sine is x
cos θ = y
θ = arccos y = cos −1 y = angle whose cosine is y
tan θ = z
θ = arctan z = tan −1 z = angle whose tangent is z

Remember that in trigonometry an expressions such as sin −1 x does not signify 1/(sin x), even though in algebra
the exponent −1 signifies a reciprocal.

PYTHAGOREAN THEOREM
The Pythagorean theorem states that the sum of the squares of the short sides of a right triangle is equal to the
square of its hypotenuse. For the triangle of Fig. 2-8,
2
2
a + b = c 2
Hence we can always express the length of any of the sides of a right triangle in terms of the lengths of the other
sides:

2
2
2
a = c − b 2 b = c − a 2 c = a + b 2
Another useful relationship is that the sum of the interior angles of any triangle is 180 . Since one of the
◦
◦
◦
angles in a right triangle is 90 , the sum of the other two must be 90 . Thus in Fig. 2-8, θ + φ = 90 .
◦
Of the six quantities that characterize a triangle—three sides and three angles—we must know the values of
at least three, including one of the sides, in order to calculate the others. In a right triangle, one of the angles is
always 90 , so all we need are the lengths of any two sides or the length of one side plus the value of one of the
◦
other angles to find the other sides and angles.