Page 227 - Schaum's Outline of Theory and Problems of Signals and Systems

216 FOURIER ANALYSIS OF TIME SIGNALS AND SYSTEMS [CHAP. 5

Therefore,

x,Jt) = lim X(k Am) ejkA"' Aw
Aw-0 2r ,= -,

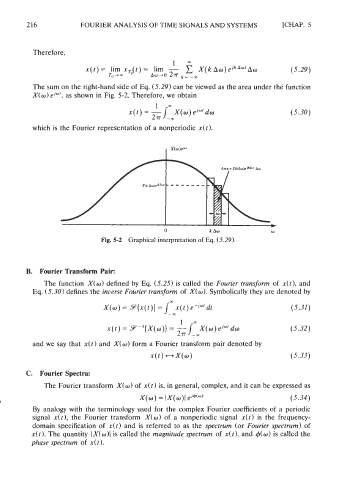
The sum on the right-hand side of Eq. (5.29) can be viewed as the area under the function
X(w) ei"', as shown in Fig. 5-2. Therefore, we obtain

which is the Fourier representation of a nonperiodic x(t).

0 k Aw w
Fig. 5-2 Graphical interpretation of Eq. (5.29).

B. Fourier Transform Pair:

The function X(o) defined by Eq. (5.25) is called the Fourier transform of x(t), and
Eq. (5.30) defines the inuerse Fourier transform of X(o). Symbolically they are denoted by

and we say that x(t) and X(w) form a Fourier transform pair denoted by

44 -X(4 (5.33)

C. Fourier Spectra:

The Fourier transform X(w) of x(t) is, in general, complex, and it can be expressed as
X(o) = (X(o)( eJd(") (5.34)
By analogy with the terminology used for the complex Fourier coefficients of a periodic
signal x(t), the Fourier transform X(w) of a nonperiodic signal x(t) is the frequency-
domain specification of x(t) and is referred to as the spectrum (or Fourier spectrum) of
x( t ). The quantity I X( w)( is called the magnitude spectrum of x(t), and $(w) is called the
phase spectrum of x(t).