Page 296 - Schaum's Outline of Theory and Problems of Signals and Systems

CHAP. 51 FOURIER ANALYSIS OF TIME SIGNALS AND SYSTEMS

Supplementary Problems

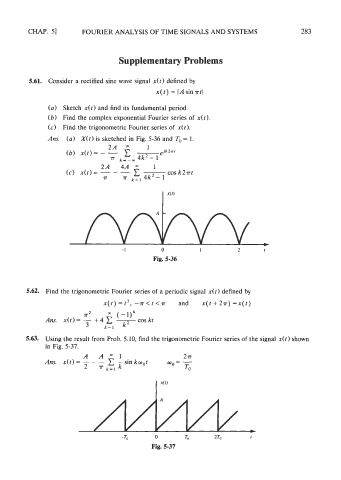
5.61. Consider a rectified sine wave signal x(t) defined by
x(l) = IAsin.srt(

(a) Sketch x(t) and find its fundamental period.
(6) Find the complex exponential Fourier series of x(!).
(c) Find the trigonometric Fourier series of x(t 1.

Am. (a) X(t) is sketched in Fig. 5-36 and T, = 1.

2A 4Am 1
(c) x(t)= - - - C -
cos k2rt
.sr IT 4k2-1

Fig. 5-36

5.62. Find the trigonometric Fourier series of a periodic signal x(t) defined by
x(t) =t2, -a < t < .rr and x(r + 2a) =x(t)

a2 a (-ilk
cos kt
Am. x(t)=- +4 -
3 k-l k
5.63. Using the result from Prob. 5.10, find the trigonometric Fourier series of the signal x(t) shown
in Fig. 5-37.
A A"1 2a
A~S. ~(t) - - - - sin ko,! wo= -
=
2 .rr &=I k To

-To 0 To 2T" r
Fig. 5-37