Page 53 - Probability, Random Variables and Random Processes

CHAP. 21 RANDOM VARIABLES

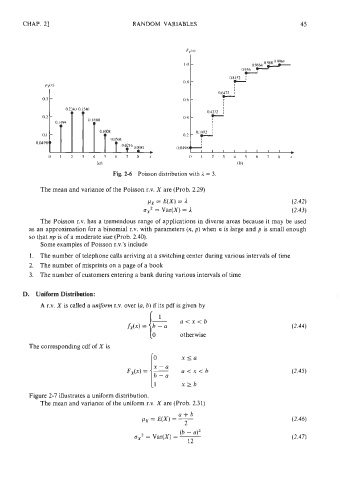
Fig. 2-6 Poisson distribution with A = 3.

The mean and variance of the Poisson r.v. X are (Prob. 2.29)
px = E(X) = A.
ax2 = Var(X) = il
The Poisson r.v. has a tremendous range of applications in diverse areas because it may be used
as an approximation for a binomial r.v. with parameters (n, p) when n is large and p is small enough
so that np is of a moderate size (Prob. 2.40).
Some examples of Poisson r.v.'s include
1. The number of telephone calls arriving at a switching center during various intervals of time
2. The number of misprints on a page of a book
3. The number of customers entering a bank during various intervals of time

D. Uniform Distribution:

A r.v. X is called a uniform r.v. over (a, b) if its pdf is given by

(0 otherwise
The corresponding cdf of X is

x-a
FX(x) = - a<x<b
{h-a

Figure 2-7 illustrates a uniform distribution.
The mean and variance of the uniform r.v. X are (Prob. 2.31)