Page 65 - Probability, Random Variables and Random Processes

CHAP. 21 RANDOM VARIABLES 5 7

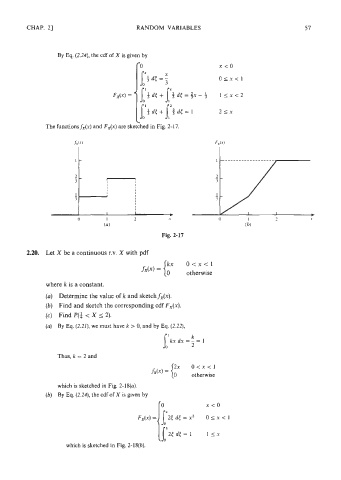
By Eq. (2.24), the cdf of X is given by X

i
3
Fix)= [idi+l$d/=%x-i 01xc1 ~ 2
~
1
5

The functions fdx) and FAX) are sketched in Fig. 2-1 7. 21x

Fig. 2-17

2.20. Let X be a continuous r.v. X with pdf
kx O<x<l
fx(x) = {O otherwise

where k is a constant.
(a) Determine the value of k and sketch f,(x).
(b) Find and sketch the corresponding cdf Fx(x).
(c) Find P($ < X 1 2).
(a) By Eq. (2.21), we must have k > 0, and by Eq. (2.22),

Thus, k = 2 and
2x O<x<l
0 otherwise
which is sketched in Fig. 2-18(a).
(b) By Eq. (2.24), the cdf of X is given by

[[2(d(=l lix
which is sketched in Fig. 2-18(b).