Page 60 - Probability, Random Variables and Random Processes

RANDOM VARIABLES [CHAP 2

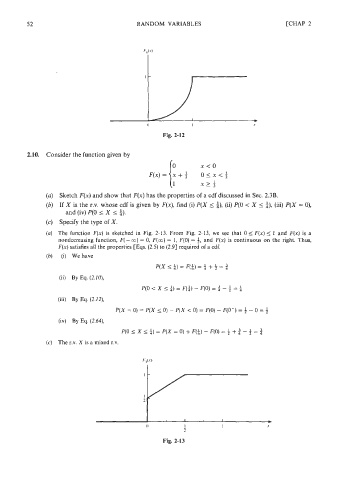
Fig. 2-12

2.10. Consider the function given by

Sketch F(x) and show that F(x) has the properties of a cdf discussed in Sec. 2.3B.
(a)
(ii)
P(0
(6) If X is the r.v. whose cdf is given by F(x), find (i) P(X I i), < X i), (iii) P(X = O),
and (iv) P(0 < X < i).
(c) Specify the type of X.
(a) The function F(x) is sketched in Fig. 2-13. From Fig. 2-13, we see that 0 < F(x) < 1 and F(x) is a
nondecreasing function, F(- co) = 0, F(co) = 1, F(0) = 4, and F(x) is continuous on the right. Thus,
F(x) satisfies all the properties [Eqs. (2.5) to (2.91 required of a cdf.
(6) (i) We have

(ii) By Eq. (2.1 O),

(iii) By Eq. (2.12),

(iv) By Eq. (2.64),

(c) The r.v. X is a mixed r.v.

Fig. 2-13