Page 141 - Sensing, Intelligence, Motion : How Robots and Humans Move in an Unstructured World

116 MOTION PLANNING FOR A MOBILE ROBOT

T T

Q
H j
L j
Q
C

T i
H j

C T i

S S
(a) (b)
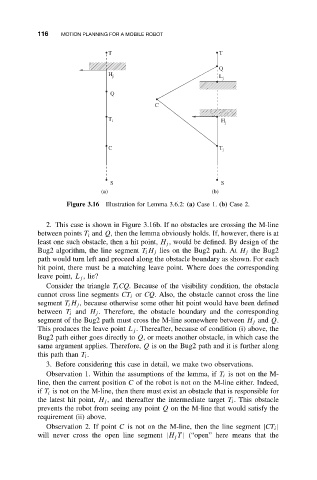
Figure 3.16 Illustration for Lemma 3.6.2: (a) Case 1. (b) Case 2.

2. This case is shown in Figure 3.16b. If no obstacles are crossing the M-line
between points T i and Q, then the lemma obviously holds. If, however, there is at
least one such obstacle, then a hit point, H j , would be defined. By design of the
Bug2 algorithm, the line segment T i H j lies on the Bug2 path. At H j the Bug2
path would turn left and proceed along the obstacle boundary as shown. For each
hit point, there must be a matching leave point. Where does the corresponding
leave point, L j , lie?
Consider the triangle T i CQ. Because of the visibility condition, the obstacle
cannot cross line segments CT i or CQ. Also, the obstacle cannot cross the line
segment T i H j , because otherwise some other hit point would have been defined
between T i and H j . Therefore, the obstacle boundary and the corresponding
segment of the Bug2 path must cross the M-line somewhere between H j and Q.
This produces the leave point L j . Thereafter, because of condition (i) above, the
Bug2 path either goes directly to Q, or meets another obstacle, in which case the
same argument applies. Therefore, Q is on the Bug2 path and it is further along
this path than T i .
3. Before considering this case in detail, we make two observations.
Observation 1. Within the assumptions of the lemma, if T i is not on the M-
line, then the current position C of the robot is not on the M-line either. Indeed,
if T i is not on the M-line, then there must exist an obstacle that is responsible for
the latest hit point, H j , and thereafter the intermediate target T i . This obstacle
prevents the robot from seeing any point Q on the M-line that would satisfy the
requirement (ii) above.
Observation 2. If point C is not on the M-line, then the line segment |CT i |
will never cross the open line segment |H j T | (“open” here means that the