Page 87 - Sensing, Intelligence, Motion : How Robots and Humans Move in an Unstructured World

62 A QUICK SKETCH OF MAJOR ISSUES IN ROBOTICS

D
G
C H J
M K
E
F I
L

A
B
(a)
D

G

H
C
E
M
I J
F L K

A B
(b)
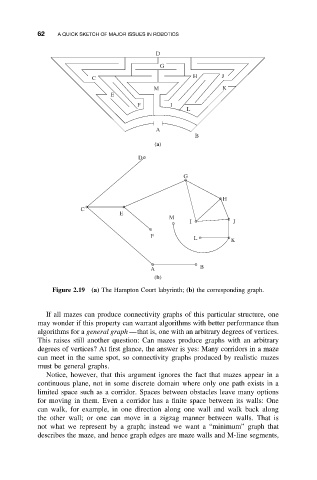
Figure 2.19 (a) The Hampton Court labyrinth; (b) the corresponding graph.

If all mazes can produce connectivity graphs of this particular structure, one
may wonder if this property can warrant algorithms with better performance than
algorithms for a general graph —that is, one with an arbitrary degrees of vertices.
This raises still another question: Can mazes produce graphs with an arbitrary
degrees of vertices? At first glance, the answer is yes: Many corridors in a maze
can meet in the same spot, so connectivity graphs produced by realistic mazes
must be general graphs.
Notice, however, that this argument ignores the fact that mazes appear in a
continuous plane, not in some discrete domain where only one path exists in a
limited space such as a corridor. Spaces between obstacles leave many options
for moving in them. Even a corridor has a finite space between its walls: One
can walk, for example, in one direction along one wall and walk back along
the other wall; or one can move in a zigzag manner between walls. That is
not what we represent by a graph; instead we want a “minimum” graph that
describes the maze, and hence graph edges are maze walls and M-line segments,