Page 88 - Sensing, Intelligence, Motion : How Robots and Humans Move in an Unstructured World

MOTION PLANNING WITH INCOMPLETE INFORMATION 63

p 2 T
H
G S
F
A
D E
p 1
C B
C
B
D
H
G
A
T E
S
F
(a) (b)
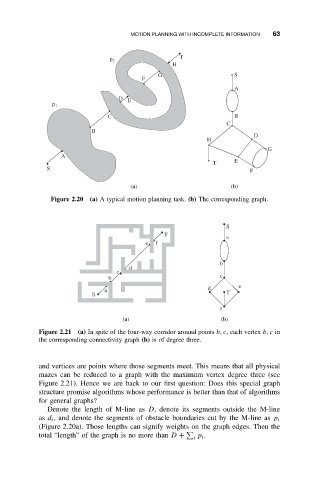
Figure 2.20 (a) A typical motion planning task. (b) The corresponding graph.

S
T a
e f

b
d
c
b c
d e
a
S T
f
(a) (b)
Figure 2.21 (a) In spite of the four-way corridor around points b, c, each vertex b, c in
the corresponding connectivity graph (b) is of degree three.

and vertices are points where those segments meet. This means that all physical
mazes can be reduced to a graph with the maximum vertex degree three (see
Figure 2.21). Hence we are back to our first question: Does this special graph
structure promise algorithms whose performance is better than that of algorithms
for general graphs?
Denote the length of M-line as D, denote its segments outside the M-line
as d i , and denote the segments of obstacle boundaries cut by the M-line as p i
(Figure 2.20a). Those lengths can signify weights on the graph edges. Then the

total “length” of the graph is no more than D + i p i .