Page 175 -

158 4. The method of multiple scales

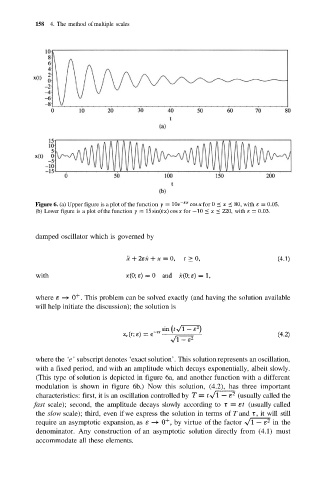
Figure 6. (a) Upper figure is a plot of the function for with
(b) Lower figure is a plot of the function for with

damped oscillator which is governed by

with

where This problem can be solved exactly (and having the solution available
will help initiate the discussion); the solution is

where the ‘e’ subscript denotes ‘exact solution’. This solution represents an oscillation,
with a fixed period, and with an amplitude which decays exponentially, albeit slowly.
(This type of solution is depicted in figure 6a, and another function with a different
modulation is shown in figure 6b.) Now this solution, (4.2), has three important
characteristics: first, it is an oscillation controlled by (usually called the
fast scale); second, the amplitude decays slowly according to (usually called
the slow scale); third, even if we express the solution in terms of T and it will still
require an asymptotic expansion, as by virtue of the factor in the
denominator. Any construction of an asymptotic solution directly from (4.1) must
accommodate all these elements.