Page 27 -

10 1. Mathematical preliminaries

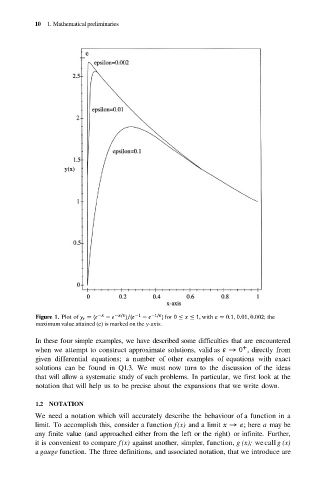
Figure 1. Plot of for with the
maximum value attained (e) is marked on the y-axis.

In these four simple examples, we have described some difficulties that are encountered
when we attempt to construct approximate solutions, valid as directly from
given differential equations; a number of other examples of equations with exact
solutions can be found in Q1.3. We must now turn to the discussion of the ideas
that will allow a systematic study of such problems. In particular, we first look at the
notation that will help us to be precise about the expansions that we write down.

1.2 NOTATION
We need a notation which will accurately describe the behaviour of a function in a
limit. To accomplish this, consider a function f (x) and a limit here a may be
any finite value (and approached either from the left or the right) or infinite. Further,
it is convenient to compare f (x) against another, simpler, function, g (x); we call g (x)
a gauge function. The three definitions, and associated notation, that we introduce are