Page 75 - Standard Handbook Of Petroleum & Natural Gas Engineering

64 Mathematics

Interpolation

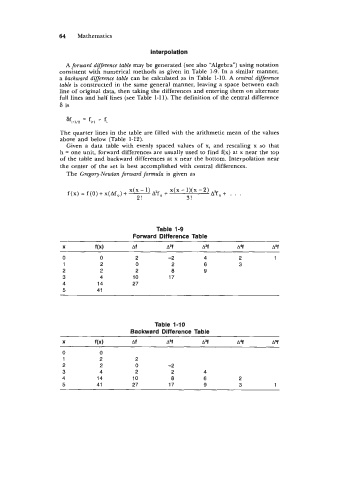
A forward difference table may be generated (see also "Algebra") using notation
consistent with numerical methods as given in Table 1-9. In a similar manner,
a backward difference table can be calculated as in Table 1-10. A central difference
table is constructed in the same general manner, leaving a space between each
line of original data, then taking the differences and entering them on alternate
full lines and half lines (see Table 1-11). The definition of the central difference
6 is

6fi+l,p = fi+, - fi
The quarter lines in the table are filled with the arithmetic mean of the values
above and below (Table 1-12).
Given a data table with evenly spaced values of x, and rescaling x so that
h = one unit, forward differences are usually used to find f(x) at x near the top
of the table and backward differences at x near the bottom. Interpolation near
the center of the set is best accomplished with central differences.
The Gregory-Newton forward formula is given as

x(x - 1) x(x-l)(x-2) 5
f(x) =f(O)+x(Af,)+- ATo + &f,+ . . .
2! 3!

Table 1-9
Forward Difference Table
foo
X Af A2f AJf AY AY
0 0 2 -2 4 2 1
1 2 0 2 6 3
2 2 2 8 9
3 4 10 17
4 14 27
5 41

Table 1-10
Backward Difference Table

0 0
1 2 2
2 2 0 -2
3 4 2 2 4
4 14 10 8 6 2
5 41 27 17 9 3 1