Page 76 - Standard Handbook Of Petroleum & Natural Gas Engineering

Numerical Methods 65

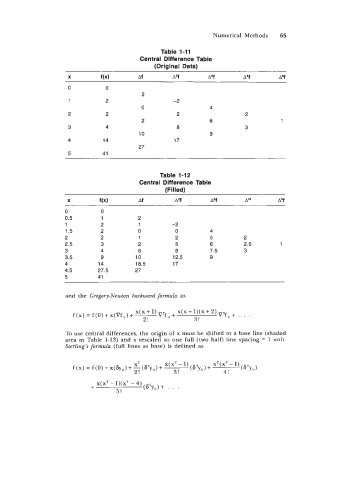
Table 1-11
Central Difference Table
(Original Data)
X f(x) Af A2f AY AV Asf
0 0
2
1 2 -2
0 4
2 2 2 2
2 6 1
3 4 8 3
10 9
4 14 17
27
5 41

Table 1-12
Central Difference Table
(Filled)

X f(x) Af A2f A3f Ad' A5f
0 0
0.5 1 2
1 2 1 -2
1.5 2 0 0 4
2 2 1 2 5 2
2.5 3 2 5 6 2.5 1
3 4 6 8 7.5 3
3.5 9 10 12.5 9
4 14 18.5 17
4.5 27.5 27
5 41

and the Gregory-Newton backward formula as

...
f(x) = f(O)+x(Vf,,)+- x(x + 1) VZf,, + x(x + l)(x + 2) VSf,, +
2! 3!
To use central differences, the origin of x must be shifted to a base line (shaded
area in Table 1-13) and x rescaled so one full (two half) line spacing = 1 unit.
Sterling's formula (full lines as base) is defined as

+ x(x* - 1)(x4 - 4)(6"")+ .
5!