Page 120 - The Combined Finite-Discrete Element Method

MUNJIZA-NBS CONTACT DETECTION ALGORITHM IN 2D 103

The aim of this section is to present an algorithm that is as efficient as the screening
algorithm in terms of CPU, and as efficient as the sorting algorithm in terms of RAM
requirements. The algorithm was developed in 1995 by Munjiza, and is called the Munjiza
No Binary Search (i.e. Munjiza-NBS) contact detection algorithm.
The Munjiza-NBS contact detection algorithm assumes a simplified contact detection
problem in 2D, i.e. a system comprising N identical discrete elements occupying a finite
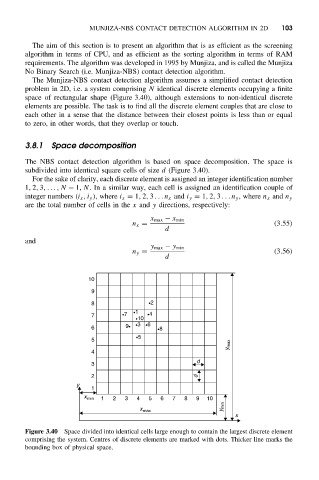
space of rectangular shape (Figure 3.40), although extensions to non-identical discrete
elements are possible. The task is to find all the discrete element couples that are close to
each other in a sense that the distance between their closest points is less than or equal
to zero, in other words, that they overlap or touch.

3.8.1 Space decomposition

The NBS contact detection algorithm is based on space decomposition. The space is
subdivided into identical square cells of size d (Figure 3.40).
For the sake of clarity, each discrete element is assigned an integer identification number
1, 2, 3,...,N − 1,N. In a similar way, each cell is assigned an identification couple of
integer numbers (i x ,i y ),where i x = 1, 2, 3 .. .n x and i y = 1, 2, 3 .. .n y ,where n x and n y
are the total number of cells in the x and y directions, respectively:

x max − x min
n x = (3.55)
d
and
y max − y min
n y = (3.56)
d

10
9
8 •2
•1
7 •7 •4
•10
6 9• •3 •6 •8
•5
5
y max
4
d
3
2 d
y
1
1 2 3 4 5 6 7 8 9 10
x min
y min
x max
x
Figure 3.40 Space divided into identical cells large enough to contain the largest discrete element
comprising the system. Centres of discrete elements are marked with dots. Thicker line marks the
bounding box of physical space.