Page 398 - The Mechatronics Handbook

In Eq. (19.12), it is assumed that the damping force on the seismic mass is proportional to velocity
only. If a harmonic vibratory motion is impressed on the instrument such that

x 1 t() = X 0 sin ( ω 1 t) (19.14)

where ω 1 is the frequency of vibration (rad/s), writing

2
d x 1
2 =
-m ---------- mX 0 sin ω 1 t
dt
modifies Eq. (19.13) as

2
d z dz
m ------- 2 + c ----- + kz mgcos= θ () + ma 1 sin ω 1 t (19.15)
dt dt
2
where a 1 = mX 0 w 1 .
Equation (19.15) will have transient and steady-state solutions. The steady-state solution of the dif-
ferential equation (19.15) may be determined as

mgcos θ () ma 1 sin ω 1 t
z = ------------------------ + ----------------------------------------- (19.16)
2
k ( k mω 1 +– jcω 1 )
Rearranging Eq. (19.16) results in

–
mgcos θ () a 1 sin ( ω 1 t φ)
z = ------------------------ + ---------------------------------------------------- (19.17)
ω n 2 2 2 2
ω n 1 r–( ) + ( 2zr)
where ω n (= k/m ) is the natural frequency of the seismic mass, V (=c/2 km ) is the damping ratio.
The damping ratio can be written in terms of the critical damping ratio as = c/c c , where c c =V 2 km ,
-1 2
φ (=tan [cω 1 /(k - mw 1 )]) is the phase angle, and r (=ω 1 /ω n ) is the frequency ratio.
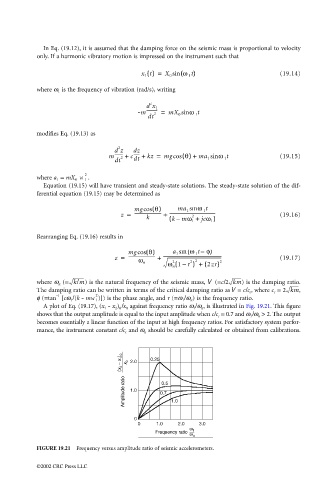
A plot of Eq. (19.17), (x 1 - x 2 ) 0 /x 0 against frequency ratio ω 1 /ω n , is illustrated in Fig. 19.21. This figure
shows that the output amplitude is equal to the input amplitude when c/c c = 0.7 and ω 1 /ω n > 2. The output
becomes essentially a linear function of the input at high frequency ratios. For satisfactory system perfor-
mance, the instrument constant c/c c and ω n should be carefully calculated or obtained from calibrations.

FIGURE 19.21 Frequency versus amplitude ratio of seismic accelerometers.

©2002 CRC Press LLC