Page 305 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

292 Vibration of Continuous Systems Chap. 9

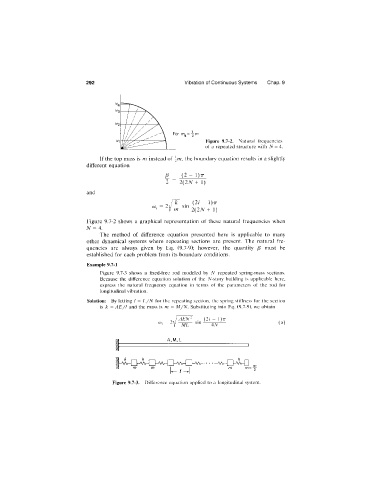
Figure 9.7-2. Natural frequencies
of a repeated structure with N = 4.
If the top mass is m instead of the boundary equation results in a slightly
different equation
( 2 - 1)TT
2 2{2N + 1)
and
(2/ — \) tt
^ 2\ — sin ^ ^ ^,
' V m 2{2N + 1)

Figure 9.7-2 shows a graphical representation of these natural frequencies when
- 4.
The method of difference equation presented here is applicable to many
other dynamical systems where repeating sections are present. The natural fre­
quencies are always given by Eq. (9.7-9); however, the quantity ¡3 must be
established for each problem from its boundary conditions.
Example 9.7-1
Figure 9.7-3 shows a fixed-free rod modeled by N repeated spring-mass sections.
Because the difference equation solution of the N-story building is applicable here,
express the natural frequency equation in terms of the param eters of the rod for
longitudinal vibration.
Solution: By letting / = L /N for the repeating section, the spring stiffness for the section
is /c = A E /l and the mass is m = M /N . Substituting into Eq. (9.7-9), we obtain

^ A E N " - . ( 2 / - 1 ) 7 7
ia, = 2\ -^rn— sm ^ ^ (a)
ME 4N
A,M,L

m m ^ ^ n i- Y

Figure 9.7-3. Difference equation applied to a longitudinal system.