Page 173 - Bird R.B. Transport phenomena

§5.2 Time-Smoothed Equations of Change for Incompressible Fluids 157

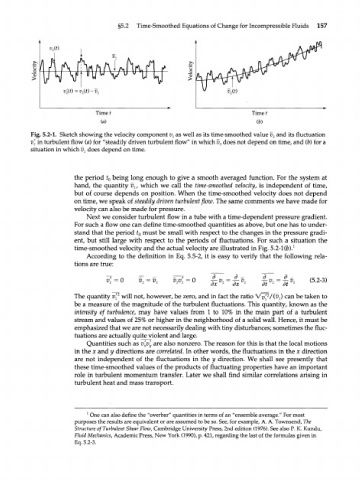
\ v z A
)city
1 U 41" и VY U
>
v' z {t) = г (t)-v z vM)
z

Timef Time t
(я) (b)
Fig. 5.2-1. Sketch showing the velocity component v z as well as its time-smoothed value v z and its fluctuation
v' in turbulent flow (a) for "steadily driven turbulent flow" in which v z does not depend on time, and (b) for a
z
situation in which v z does depend on time.

the period f being long enough to give a smooth averaged function. For the system at
0
hand, the quantity v , which we call the time-smoothed velocity, is independent of time,
z
but of course depends on position. When the time-smoothed velocity does not depend
on time, we speak of steadily driven turbulent flow. The same comments we have made for
velocity can also be made for pressure.
Next we consider turbulent flow in a tube with a time-dependent pressure gradient.
For such a flow one can define time-smoothed quantities as above, but one has to under-
stand that the period t 0 must be small with respect to the changes in the pressure gradi-
ent, but still large with respect to the periods of fluctuations. For such a situation the
time-smoothed velocity and the actual velocity are illustrated in Fig. 5.2-1 (b). 1
According to the definition in Eq. 5.5-2, it is easy to verify that the following rela-
tions are true:
д -
= v z v (5.2-3)

2
The quantity v' will not, however, be zero, and in fact the ratio V^V(i> ) can be taken to
z
2
be a measure of the magnitude of the turbulent fluctuations. This quantity, known as the
intensity of turbulence, may have values from 1 to 10% in the main part of a turbulent
stream and values of 25% or higher in the neighborhood of a solid wall. Hence, it must be
emphasized that we are not necessarily dealing with tiny disturbances; sometimes the fluc-
tuations are actually quite violent and large.
Quantities such as v' v' are also nonzero. The reason for this is that the local motions
y
x
in the x and у directions are correlated. In other words, the fluctuations in the x direction
are not independent of the fluctuations in the у direction. We shall see presently that
these time-smoothed values of the products of fluctuating properties have an important
role in turbulent momentum transfer. Later we shall find similar correlations arising in
turbulent heat and mass transport.

1 One can also define the "overbar" quantities in terms of an "ensemble average." For most
purposes the results are equivalent or are assumed to be so. See, for example, A. A. Townsend, The
Structure of Turbulent Shear Flow, Cambridge University Press, 2nd edition (1976). See also P. K. Kundu,
Fluid Mechanics, Academic Press, New York (1990), p. 421, regarding the last of the formulas given in
Eq. 5.2-3.