Page 19 - Bird R.B. Transport phenomena

4 Chapter 0 The Subject of Transport Phenomena

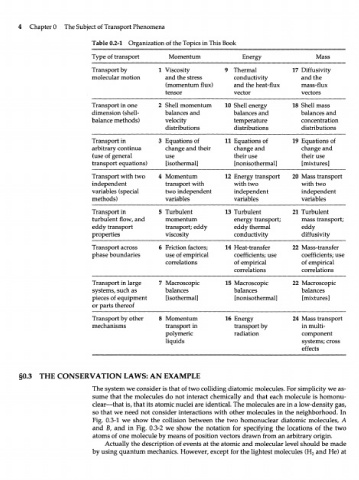
Table 0.2-1 Organization of the Topics in This Book
Type of transport Momentum Energy Mass
Transport by 1 Viscosity 9 Thermal 17 Diffusivity
molecular motion and the stress conductivity and the
(momentum flux) and the heat-flux mass-flux
tensor vector vectors

Transport in one 2 Shell momentum 10 Shell energy 18 Shell mass
dimension (shell- balances and balances and balances and
balance methods) velocity temperature concentration
distributions distributions distributions
Transport in 3 Equations of 11 Equations of 19 Equations of
arbitrary continua change and their change and change and
(use of general use their use their use
transport equations) [isothermal] [nonisothermal] [mixtures]
Transport with two 4 Momentum 12 Energy transport 20 Mass transport
independent transport with with two with two
variables (special two independent independent independent
methods) variables variables variables
Transport in 5 Turbulent 13 Turbulent 21 Turbulent
turbulent flow, and momentum energy transport; mass transport;
eddy transport transport; eddy eddy thermal eddy
properties viscosity conductivity diffusivity

Transport across 6 Friction factors; 14 Heat-transfer 22 Mass-transfer
phase boundaries use of empirical coefficients; use coefficients; use
correlations of empirical of empirical
correlations correlations
Transport in large 7 Macroscopic 15 Macroscopic 22 Macroscopic
systems, such as balances balances balances
pieces of equipment [isothermal] [nonisothermal] [mixtures]
or parts thereof
Transport by other 8 Momentum 16 Energy 24 Mass transport
mechanisms transport in transport by in multi-
polymeric radiation component
liquids systems; cross
effects

§0.3 THE CONSERVATION LAWS: AN EXAMPLE
The system we consider is that of two colliding diatomic molecules. For simplicity we as-
sume that the molecules do not interact chemically and that each molecule is homonu-
clear—that is, that its atomic nuclei are identical. The molecules are in a low-density gas,
so that we need not consider interactions with other molecules in the neighborhood. In
Fig. 0.3-1 we show the collision between the two homonuclear diatomic molecules, A
and B, and in Fig. 0.3-2 we show the notation for specifying the locations of the two
atoms of one molecule by means of position vectors drawn from an arbitrary origin.
Actually the description of events at the atomic and molecular level should be made
by using quantum mechanics. However, except for the lightest molecules (H 2 and He) at