Page 198 - Bird R.B. Transport phenomena

182 Chapter 6 Interphase Transport in Isothermal Systems

1.0

0.5

0.2

0.1 \
ч-/
| 0.05 \
j
о s
I 0.02 s
TurbulerIt
\
0.01
::k/D = 0.0 )4
4 1 •• • m Si - *—0.C)0(31
0.005 ft 0.001
O.OOC4
0.002 kcallys •*——4—^ нu..
'ЛОС
> ч r
0.001
10 3 10 4 10 5 10 6 10 7
Reynolds number Re = D<v> p/fi
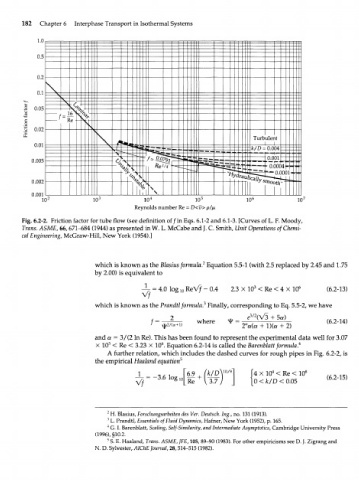
Fig. 6.2-2. Friction factor for tube flow (see definition of/in Eqs. 6.1-2 and 6.1-3. [Curves of L. F. Moody,
Trans. ASME, 66, 671-684 (1944) as presented in W. L. McCabe and J. C. Smith, Unit Operations of Chemi-
cal Engineering, McGraw-Hill, New York (1954).]

2
which is known as the Blasius formula. Equation 5.5-1 (with 2.5 replaced by 2.45 and 1.75
by 2.00) is equivalent to
- y = 4.0 log ReV7 - 0.4 2.3 X 10 3 < Re < 4 X 10 6 (6.2-13)
10
3
which is known as the Prandtl formula. Finally, corresponding to Eq. 5.5-2, we have
5a)
where (6.2-14)
J ^2/(a + i) 2 a{a + \){a + 2)
a
and a = 3/(2 In Re). This has been found to represent the experimental data well for 3.07
6
X 10 3 < Re < 3.23 X 10 . Equation 6.2-14 is called the Barenblatt formula*
A further relation, which includes the dashed curves for rough pipes in Fig. 6.2-2, is
the empirical Haaland equation 5
4
* * i
4_ (k/D\°' ~]
Гб.9
1
[
— =-3.6 log ф ^ — J 9 J [4XlO <Re <10 8 (6.2-15)
0<k/D<0j 0.05
2
H. Blasius, Forschungsarbeiten des Ver. Deutsch. Ing., no. 131 (1913).
L. Prandtl, Essentials of Fluid Dynamics, Hafner, New York (1952), p. 165.
3
4 G. I. Barenblatt, Scaling, Self-Similarity, and Intermediate Asymptotics, Cambridge University Press
(1996), §10.2.
5
S. E. Haaland, Trans. ASME, JFE, 105, 89-90 (1983). For other empiricisms see D. J. Zigrang and
N. D. Sylvester, AIChE Journal, 28, 514-515 (1982).