Page 203 - Bird R.B. Transport phenomena

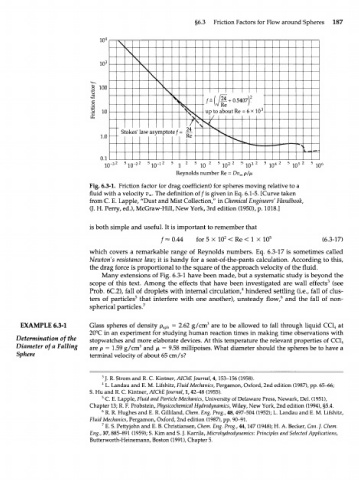
§6.3 Friction Factors for Flow around Spheres 187

1U
\
\
10 3
\
\ \
)n factor / о о \ s

."5 ю UP to a b n n f TCP> — f\ X 1 Г)3.
s i/
/ N ч
1
Stokes law asymptote f=^-
1.0
- ——• 55ИВ—
0.1
10 _ 3 2 5 10 _ 2 2 5 l 2 5 1 Q 2 5 ^ 2 2 5 ^ 5 ] ( ) 6
Reynolds number Re = Dv x р//л

Fig. 6.3-1. Friction factor (or drag coefficient) for spheres moving relative to a
fluid with a velocity v . The definition of/is given in Eq. 6.1-5. [Curve taken
x
from С. Е. Lapple, "Dust and Mist Collection/' in Chemical Engineers Handbook,
(J. H. Perry, ed.), McGraw-Hill, New York, 3rd edition (1950), p. 1018.]

is both simple and useful. It is important to remember that
f - 0.44 for 5 X 10 2 < Re < 1 X 10 5 (6.3-17)

which covers a remarkable range of Reynolds numbers. Eq. 6.3-17 is sometimes called
Newton's resistance law; it is handy for a seat-of-the-pants calculation. According to this,
the drag force is proportional to the square of the approach velocity of the fluid.
Many extensions of Fig. 6.3-1 have been made, but a systematic study is beyond the
scope of this text. Among the effects that have been investigated are wall effects 3 (see
Prob. 6C.2), fall of droplets with internal circulation, hindered settling (i.e., fall of clus-
4
ters of particles 5 that interfere with one another), unsteady flow, 6 and the fall of non-
spherical particles. 7

EXAMPLE 6.3-1 Glass spheres of density p sph = 2.62 g/cm 3 are to be allowed to fall through liquid CC1 at
4
20°C in an experiment for studying human reaction times in making time observations with
Determination of the stopwatches and more elaborate devices. At this temperature the relevant properties of CC1
Diameter of availing are p = 1.59 g/cm 3 and /л = 9.58 millipoises. What diameter should the spheres be to have a 4
Sphere terminal velocity of about 65 cm/s?

J. R. Strom and R. C. Kintner, AIChE Journal, 4,153-156 (1958).
3
4
L. Landau and E. M. Lifshitz, Fluid Mechanics, Pergamon, Oxford, 2nd edition (1987), pp. 65-66;
S. Hu and R. C. Kintner, AIChE Journal, 1,42-48 (1955).
С. Е. Lapple, Fluid and Particle Mechanics, University of Delaware Press, Newark, Del. (1951),
5
Chapter 13; R. F. Probstein, Physicochemical Hydrodynamics, Wiley, New York, 2nd edition (1994), §5.4.
6
R. R. Hughes and E. R. Gilliland, Chem. Eng. Prog., 48,497-504 (1952); L. Landau and E. M. Lifshitz,
Fluid Mechanics, Pergamon, Oxford, 2nd edition (1987), pp. 90-91.
E. S. Pettyjohn and E. B. Christiansen, Chem. Eng. Prog., 44,147 (1948); H. A. Becker, Can. J. Chem.
7
Eng., 37, 885-891 (1959); S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications,
Butterworth-Heinemann, Boston (1991), Chapter 5.