Page 358 - Bird R.B. Transport phenomena
P. 358
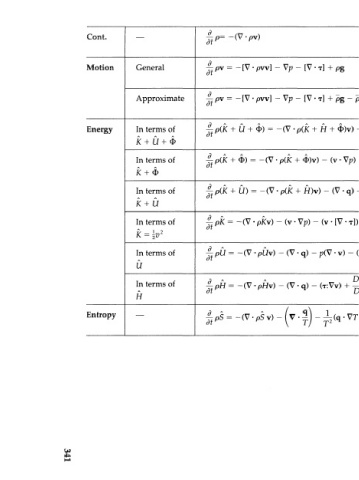
Cont. — | p = - ( V - p v ) 3.1-4 For p = constant, simplifies to
(K) (V • v) = 0
Motion General jpv= -[V-pw]-Vp-[V- ] + pg 3.2-9 For т = 0 this becomes Euler's
t T
(L) equation
Approximate j pv = -[V • pvv] - Vp - [V • T] + pg - pg/3(T - T) Displays buoyancy term
t
(M)
Energy In terms of ^p(X+ 1> + Ф) = -(V-p(K + H + <I>)v)-(V«q)-(V4T-v]) 11.1-9 Exact only for Ф time independent
X+ й + Ф ot (N)
In terms of j-p(K + Ф) = -(V-p(X + Ф)у) - ( v Vp) - ( v [V-T]) 3.3-2 Exact only for Ф time independent
t
K + Ф (O) From equation of motion
In terms of j t p(K + II) = - (V • p(X + H)v) - (V • q) - (V • [T • v)] + p(v • g)11.1-7
X+ U (P)
In terms of j t pK = - (V • pkv) - (v • Vp) - (v • [V • T]) 4- p(v • g) 3.3-1 From equation of motion
к = h 2 (Q)
In terms of ^ pQ = -(V • pUv) - (V • q) - p(V • v) - (T:VV) 11.2-1 Term containing (V • v) is zero for
U (R) constant p
In terms of ^ p H = -(V-pHv) - (V • q) - (T:VV) + Щ H = U + {pip)
H (S)
Entropy — fpS = -(V-pSv) " (^ - | ) - ^ ( q - VT) - 1(T:VV) 11D.1-1 Last two terms describe entropy
t
(T) production