Page 364 - Bird R.B. Transport phenomena

346 Chapter 11 The Equations of Change for Nonisothermal Systems

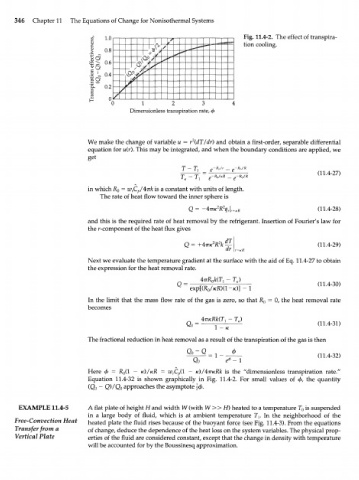
i w Fig. 11.4-2. The effect of transpira-
tion cooling.
с ***
£ 0.8 <**
0.6 ( i /
U° A A r

'Цг 0.2 /
у
1 2 3
Dimensionless transpiration rate, ф

We make the change of variable и = r\dT/dr) and obtain a first-order, separable differential
equation for u(r). This may be integrated, and when the boundary conditions are applied, we
get
T -
(11.4-27)

in which R o = zv C /47rk is a constant with units of length.
p
r
The rate of heat flow toward the inner sphere is
2
Q = -47TK R\\ r , KR (11.4-28)
and this is the required rate of heat removal by the refrigerant. Insertion of Fourier's law for
the r-component of the heat flux gives

(11.4-29)
dr
Next we evaluate the temperature gradient at the surface with the aid of Eq. 11.4-27 to obtain
the expression for the heat removal rate.
- T K )
T }
Q = (11.4-30)
exp[(R 0/#c£)(l-#c)]-l
In the limit that the mass flow rate of the gas is zero, so that R o = 0, the heat removal rate
becomes
4777СЩТ! - Т к )
1 - к (11.4-31)
The fractional reduction in heat removal as a result of the transpiration of the gas is then
Qo-Q Ф
1 (11.4-32)
Qo
Here ф = R (l - K)/KR = w,.C (l - к)/4тгкЯк is the "dimensionless transpiration rate."
0
p
Equation 11.4-32 is shown graphically in Fig. 11.4-2. For small values of ф, the quantity
(Qo - Q)/Qo approaches the asymptote \ф.
EXAMPLE 11.4-5 A flat plate of height H and width W (with W» H) heated to a temperature T is suspended
o
in a large body of fluid, which is at ambient temperature T . In the neighborhood of the
}
Free-Convection Heat heated plate the fluid rises because of the buoyant force (see Fig. 11.4-3). From the equations
Transfer from a of change, deduce the dependence of the heat loss on the system variables. The physical prop-
Vertical Plate erties of the fluid are considered constant, except that the change in density with temperature
will be accounted for by the Boussinesq approximation.