Page 371 - Bird R.B. Transport phenomena

§11.5 Dimensional Analysis of the Equations of Change for Nonisothermal Systems 353

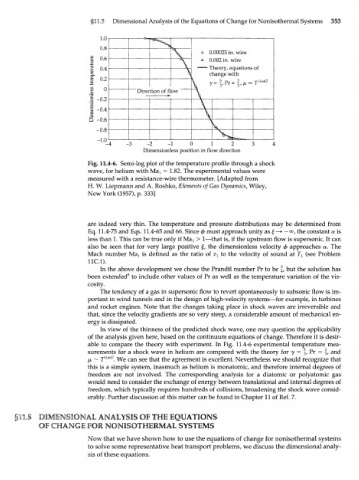
T о 0.00025 in. wire
\
\ — A 0.002 in. wire
Theory,
equations of
change with
V r-i.p'-f.».- j 0.647
Direction of flow
3"

h - >

-4 -3 - 2 - 1 0 1 2
Dimensionless position in flow direction
Fig. 11.4-6. Semi-log plot of the temperature profile through a shock
wave, for helium with Мат = 1.82. The experimental values were
measured with a resistance-wire thermometer. [Adapted from
H. W. Liepmann and A. Roshko, Elements of Gas Dynamics, Wiley,
New York (1957), p. 333]

are indeed very thin. The temperature and pressure distributions may be determined from
Eq. 11.4-75 and Eqs. 11.4-65 and 66. Since ф must approach unity as £ —> -°°, the constant a is
less than 1. This can be true only if Мат > 1—that is, if the upstream flow is supersonic. It can
also be seen that for very large positive £, the dimensionless velocity ф approaches a. The
Mach number Ma] is defined as the ratio of v } to the velocity of sound at Tj (see Problem
11C.1).
In the above development we chose the Prandtl number Pr to be \, but the solution has
been extended 8 to include other values of Pr as well as the temperature variation of the vis-
cosity.
The tendency of a gas in supersonic flow to revert spontaneously to subsonic flow is im-
portant in wind tunnels and in the design of high-velocity systems—for example, in turbines
and rocket engines. Note that the changes taking place in shock waves are irreversible and
that, since the velocity gradients are so very steep, a considerable amount of mechanical en-
ergy is dissipated.
In view of the thinness of the predicted shock wave, one may question the applicability
of the analysis given here, based on the continuum equations of change. Therefore it is desir-
able to compare the theory with experiment. In Fig. 11.4-6 experimental temperature mea-
surements for a shock wave in helium are compared with the theory for у = |, Pr = §, and
647
ix ~ T° . We can see that the agreement is excellent. Nevertheless we should recognize that
this is a simple system, inasmuch as helium is monatomic, and therefore internal degrees of
freedom are not involved. The corresponding analysis for a diatomic or polyatomic gas
would need to consider the exchange of energy between translational and internal degrees of
freedom, which typically requires hundreds of collisions, broadening the shock wave consid-
erably. Further discussion of this matter can be found in Chapter 11 of Ref. 7.

511.5 DIMENSIONAL ANALYSIS OF THE EQUATIONS
OF CHANGE FOR NONISOTHERMAL SYSTEMS

Now that we have shown how to use the equations of change for nonisothermal systems
to solve some representative heat transport problems, we discuss the dimensional analy-
sis of these equations.