Page 375 - Bird R.B. Transport phenomena

§11.5 Dimensional Analysis of the Equations of Change for Nonisothermal Systems 357

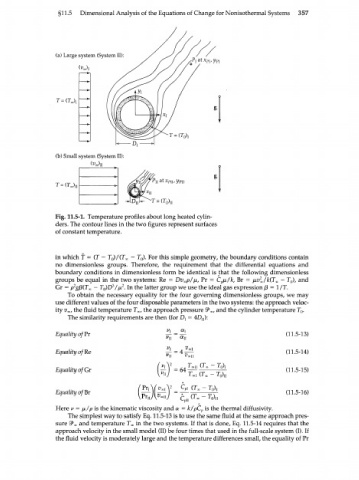
(a) Large system (System

(b) Small system (System II):

T=(TJ

Fig. 11.5-1. Temperature profiles about long heated cylin-
ders. The contour lines in the two figures represent surfaces
of constant temperature.

in which f = (T - T )/(T X - T ). For this simple geometry, the boundary conditions contain
Q
o
no dimensionless groups. Therefore, the requirement that the differential equations and
boundary conditions in dimensionless form be identical is that the following dimensionless
2
groups be equal in the two systems: Re = Dv p/\x, Pr = C /x/k, Br = iJLV /k(T x - T ), and
p
x
o
oo
2
2
Gr = p gf3(T x - T )DV/x . In the latter group we use the ideal gas expression /3 = 1/Г.
0
To obtain the necessary equality for the four governing dimensionless groups, we may
use different values of the four disposable parameters in the two systems: the approach veloc-
ity v , the fluid temperature T , the approach pressure & , and the cylinder temperature T .
o
x
x
K
The similarity requirements are then (for Dj = 4D ):
n
Equality of Pr (11.5-13)
«II
Equality of Re (11.5-14)
*>»ii
T^
Equality of Gr = 64 (П.5-15)
Too, (T« "
Pr, C,i (T. -
Equality of Br (11.5-16)
Pr,, с (г--г„)„
-pll
я11
Here v = fi/p is the kinematic viscosity and o: = k/pC is the thermal diffusivity.
p
The simplest way to satisfy Eq. 11.5-13 is to use the same fluid at the same approach pres-
sure & x and temperature T x in the two systems. If that is done, Eq. 11.5-14 requires that the
approach velocity in the small model (II) be four times that used in the full-scale system (I). If
the fluid velocity is moderately large and the temperature differences small, the equality of Pr