Page 520 - Bird R.B. Transport phenomena

500 Chapter 16 Energy Transport by Radiation

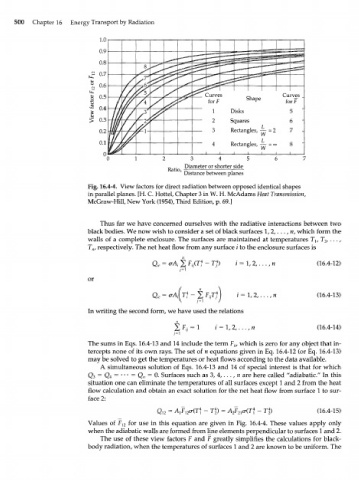
3 4 5
Diameter or shorter side
Ratio,
Distance between planes
Fig. 16.4-4. View factors for direct radiation between opposed identical shapes
in parallel planes. [H. C. Hottel, Chapter 3 in W. H. McAdams Heat Transmission,
McGraw-Hill, New York (1954), Third Edition, p. 69.]

Thus far we have concerned ourselves with the radiative interactions between two
black bodies. We now wish to consider a set of black surfaces 1,2,..., w, which form the
walls of a complete enclosure. The surfaces are maintained at temperatures T u T ,...,
2
T , respectively. The net heat flow from any surface i to the enclosure surfaces is
n
i = 1,2,..., n (16.4-12)

or

Q k = X i = \,2 n (16.4-13)
In writing the second form, we have used the relations

n
2 F /7 = 1 i = 1, ,..., n (16.4-14)
2
The sums in Eqs. 16.4-13 and 14 include the term F , which is zero for any object that in-
u
tercepts none of its own rays. The set of n equations given in Eq. 16.4-12 (or Eq. 16.4-13)
may be solved to get the temperatures or heat flows according to the data available.
A simultaneous solution of Eqs. 16.4-13 and 14 of special interest is that for which
Q3 = QA = ''' = Qn = 0- Surfaces such as 3, ,..., n are here called "adiabatic." In this
4
situation one can eliminate the temperatures of all surfaces except 1 and 2 from the heat
flow calculation and obtain an exact solution for the net heat flow from surface 1 to sur-
face 2:

Q = ~ П) = ~ П) (16.4-15)
12
Values of F 12 for use in this equation are given in Fig. 16.4-4. These values apply only
when the adiabatic walls are formed from line elements perpendicular to surfaces 1 and 2.
The use of these view factors F and F greatly simplifies the calculations for black-
body radiation, when the temperatures of surfaces 1 and 2 are known to be uniform. The