Page 515 - Bird R.B. Transport phenomena

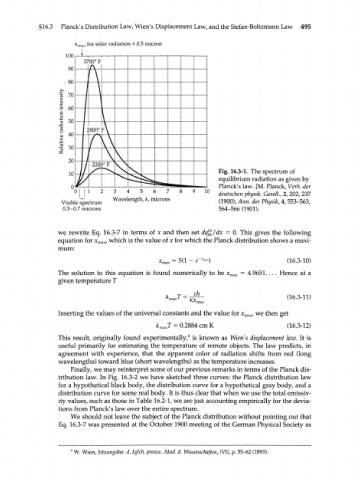
§16.3 Planck's Distribution Law, Wien's Displacement Law, and the Stefan-Boltzmann Law 495

A max for solar radiation = 0.5 micron

Fig. 16.3-1. The spectrum of
equilibrium radiation as given by
Planck's law. [M. Planck, Verh. der
3 4 5 6 7 10 deutschen physik. GeselL, 2,202,237
Visible spectrum Wavelength, A, microns (1900); Ann. der Physik, 4,553-563,
0.3-0.7 microns 564-566 (1901).

we rewrite Eq. 16.3-7 in terms of x and then set dq^l/dx = 0. This gives the following
equation for x , which is the value of x for which the Planck distribution shows a maxi-
max
mum:
W = 5(1 - «-'-) (16.3-10)

The solution to this equation is found numerically to be x max = 4.9651. ,.. Hence at a
given temperature T

X T - ch (16.3-11)
m a x
Inserting the values of the universal constants and the value for x max , we then get
A ^ = 0.2884 cm К (16.3-12)
max
This result, originally found experimentally, 6 is known as Wien's displacement law. It is
useful primarily for estimating the temperature of remote objects. The law predicts, in
agreement with experience, that the apparent color of radiation shifts from red (long
wavelengths) toward blue (short wavelengths) as the temperature increases.
Finally, we may reinterpret some of our previous remarks in terms of the Planck dis-
tribution law. In Fig. 16.3-2 we have sketched three curves: the Planck distribution law
for a hypothetical black body, the distribution curve for a hypothetical gray body, and a
distribution curve for some real body. It is thus clear that when we use the total emissiv-
ity values, such as those in Table 16.2-1, we are just accounting empirically for the devia-
tions from Planck's law over the entire spectrum.
We should not leave the subject of the Planck distribution without pointing out that
Eq. 16.3-7 was presented at the October 1900 meeting of the German Physical Society as

6
W. Wien, Sitzungsber. d. kglch. preuss. Akad. d. Wissenschaften, (VI), p. 55-62 (1893).