Page 59 - Tribology in Machine Design

46 Tribology in machine design

A non-dimensional normal stress T can be defined as

The shear stress acting at the same point is

and the corresponding nondimensional stress is

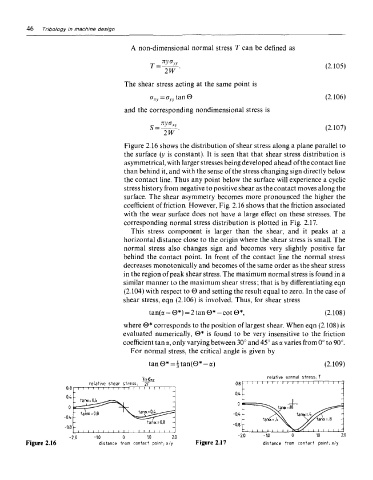
Figure 2.16 shows the distribution of shear stress along a plane parallel to
the surface (y is constant). It is seen that that shear stress distribution is
asymmetrical, with larger stresses being developed ahead of the contact line
than behind it, and with the sense of the stress changing sign directly below
the contact line. Thus any point below the surface will experience a cyclic
stress history from negative to positive shear as the contact moves along the
surface. The shear asymmetry becomes more pronounced the higher the
coefficient of friction. However, Fig. 2.16 shows that the friction associated
with the wear surface does not have a large effect on these stresses. The
corresponding normal stress distribution is plotted in Fig. 2.17.
This stress component is larger than the shear, and it peaks at a
horizontal distance close to the origin where the shear stress is small. The
normal stress also changes sign and becomes very slightly positive far
behind the contact point. In front of the contact line the normal stress
decreases monotonically and becomes of the same order as the shear stress
in the region of peak shear stress. The maximum normal stress is found in a
similar manner to the maximum shear stress; that is by differentiating eqn
(2.104) with respect to 0 and setting the result equal to zero. In the case of
shear stress, eqn (2.106) is involved. Thus, for shear stress

where 0* corresponds to the position of largest shear. When eqn (2.108) is
evaluated numerically, 0* is found to be very insensitive to the friction
coefficient tan a, only varying between 30° and 45° as a varies from 0° to 90°.
For normal stress, the critical angle is given by

Figure 2.16 Figure 2.17