Page 133 - Video Coding for Mobile Communications Efficiency, Complexity, and Resilience

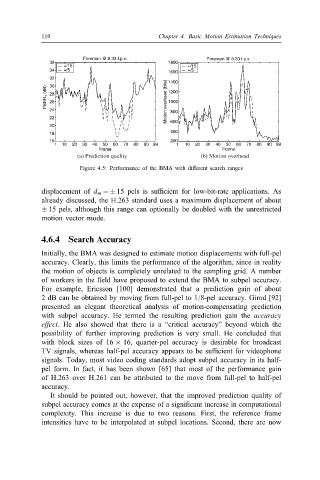
110 Chapter 4. Basic Motion Estimation Techniques

Foreman @ 8.33 f.p.s. Foreman @ 8.33 f.p.s.
36 1800
+/15 +/15
34 +/5 +/5
1600
32 1400
PSNR Y (dB) 28 Motion overhead (bits) 1200
30
1000
26
24 800
22 600
20
18 400
16 200
1 10 20 30 40 50 60 70 80 90 99 1 10 20 30 40 50 60 70 80 90 99
Frame Frame
(a) Prediction quality (b) Motion overhead
Figure 4.5: Performance of the BMA with di erent search ranges

displacement of d m = ± 15 pels is su!cient for low-bit-rate applications. As
already discussed, the H.263 standard uses a maximum displacement of about
± 15 pels, although this range can optionally be doubled with the unrestricted
motion vector mode.

4.6.4 Search Accuracy

Initially, the BMA was designed to estimate motion displacements with full-pel
accuracy. Clearly, this limits the performance of the algorithm, since in reality
the motion of objects is completely unrelated to the sampling grid. A number
of workers in the eld have proposed to extend the BMA to subpel accuracy.
For example, Ericsson [100] demonstrated that a prediction gain of about
2 dB can be obtained by moving from full-pel to 1=8-pel accuracy. Girod [92]
presented an elegant theoretical analysis of motion-compensating prediction
with subpel accuracy. He termed the resulting prediction gain the accuracy
e ect. He also showed that there is a “critical accuracy” beyond which the
possibility of further improving prediction is very small. He concluded that
with block sizes of 16 × 16, quarter-pel accuracy is desirable for broadcast
TV signals, whereas half-pel accuracy appears to be su!cient for videophone
signals. Today, most video coding standards adopt subpel accuracy in its half-
pel form. In fact, it has been shown [65] that most of the performance gain
of H.263 over H.261 can be attributed to the move from full-pel to half-pel
accuracy.
It should be pointed out, however, that the improved prediction quality of
subpel accuracy comes at the expense of a signi cant increase in computational
complexity. This increase is due to two reasons. First, the reference frame
intensities have to be interpolated at subpel locations. Second, there are now