Page 521 - Water and wastewater engineering

13-16 WATER AND WASTEWATER ENGINEERING

The Chick-Watson law assumes that the concentration of disinfectant remains constant. As
noted above, even without reaction with other constituents in the water, the disinfectant con-
centration decays with time. Even if the concentration is kept constant during inactivation of
microorganisms, the results do not always follow Equation 13-23 . “Tailing,” “shoulders,” and
time lags may occur with different microorganism and disinfectant combinations. Different tem-
peratures and pH values for the same organism and disinfectant will result in different curves as
shown in Figures 13-4a and 13-4b .
In many cases the exponent “ n ” in Equation 13-22 is close to 1.0 (Hoff, 1986). Thus, a fixed
value of the product Ct results in a fixed degree of inactivation.
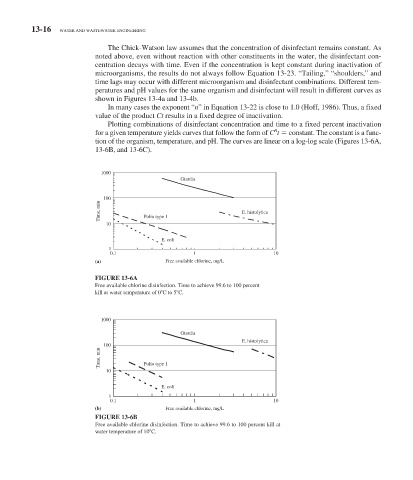
Plotting combinations of disinfectant concentration and time to a fixed percent inactivation
n
for a given temperature yields curves that follow the form of C t constant. The constant is a func-
tion of the organism, temperature, and pH. The curves are linear on a log-log scale ( Figures 13-6 A,
13-6B, and 13-6C).

1000
Giardia

100
Time, min Polio type 1 E. histolytica

10
E. coli
1
0.1 1 10
(a) Free available chlorine, mg/L

FIGURE 13-6A
Free available chlorine disinfection. Time to achieve 99.6 to 100 percent
kill at water temperature of 0 C to 5 C.

1000

Giardia
E. histolytica
100
Time, min Polio type 1

10

E. coli
1
0.1 1 10
(b) Free available chlorine, mg/L
FIGURE 13-6B
Free available chlorine disinfection. Time to achieve 99.6 to 100 percent kill at
water temperature of 10 C.