Page 42 - Fluid Power Engineering

20 Chapter Tw o

Power Coefficient
0.7
0.6

0.5

0.4
0.3

0.2

0.1
0
0 0.1 0.2 0.3 0.33333 0.4 0.5 0.6 0.7 0.8 0.9 1

v 2 /v 0
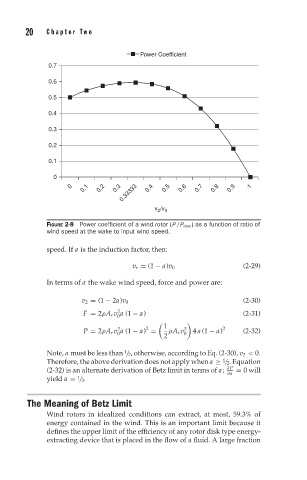
FIGURE 2-8 Power coefficient of a wind rotor (P/P ideal ) as a function of ratio of
wind speed at the wake to input wind speed.

speed. If a is the induction factor, then:

v r = (1 − a)v 0 (2-29)

In terms of a the wake wind speed, force and power are:

v 2 = (1 − 2a)v 0 (2-30)
2
F = 2ρA r v a (1 − a) (2-31)
0

3 2 1 3 2
P = 2ρA r v a (1 − a) = ρA r v 0 4 a (1 − a) (2-32)
0
2
1
Note, a must be less than / 2, otherwise, according to Eq. (2-30), v 2 < 0.
Therefore, the above derivation does not apply when a ≥ / 2. Equation
1
(2-32) is an alternate derivation of Betz limit in terms of a; ∂ P = 0 will
∂a
yield a = / 3.
1
The Meaning of Betz Limit
Wind rotors in idealized conditions can extract, at most, 59.3% of
energy contained in the wind. This is an important limit because it
defines the upper limit of the efficiency of any rotor disk type energy-
extracting device that is placed in the flow of a fluid. A large fraction