Page 229 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

QC: IML/FFX
T1: IML
P1: IML/FFX
P2: IML/FFX
August 16, 2007
17:42
AT029-Manual-v7.cls
AT029-05
AT029-Manual
5. PVT RELATIONS AND EQUATIONS OF STATE 209

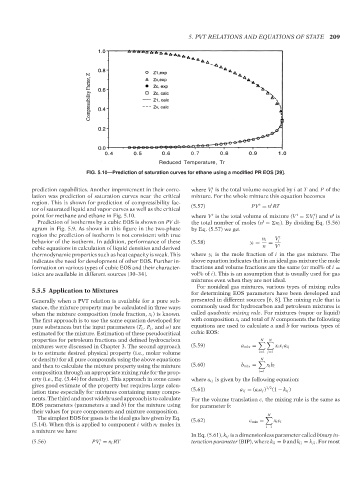
FIG. 5.10—Prediction of saturation curves for ethane using a modified PR EOS [29].

prediction capabilities. Another improvement in their corre- where V is the total volume occupied by i at T and P of the
t
i
lation was prediction of saturation curves near the critical mixture. For the whole mixture this equation becomes
region. This is shown for prediction of compressibility fac- t t
tor of saturated liquid and vapor curves as well as the critical (5.57) PV = n RT
t
t
point for methane and ethane in Fig. 5.10. where V is the total volume of mixture (V = V ) and n is
t
t
i
t
Prediction of isotherms by a cubic EOS is shown on PV di- the total number of moles (n = n i ). By dividing Eq. (5.56)
agram in Fig. 5.9. As shown in this figure in the two-phase by Eq. (5.57) we get
region the prediction of isotherm is not consistent with true t
behavior of the isotherm. In addition, performance of these (5.58) y i = n i = V i t
cubic equations in calculation of liquid densities and derived n V
thermodynamic properties such as heat capacity is weak. This where y i is the mole fraction of i in the gas mixture. The
indicates the need for development of other EOS. Further in- above equation indicates that in an ideal gas mixture the mole
formation on various types of cubic EOS and their character- fractions and volume fractions are the same (or mol% of i =
istics are available in different sources [30–34]. vol% of i). This is an assumption that is usually used for gas
mixtures even when they are not ideal.
For nonideal gas mixtures, various types of mixing rules
5.5.5 Application to Mixtures for determining EOS parameters have been developed and
Generally when a PVT relation is available for a pure sub- presented in different sources [6, 8]. The mixing rule that is
stance, the mixture property may be calculated in three ways commonly used for hydrocarbon and petroleum mixtures is
when the mixture composition (mole fraction, x i ) is known. called quadratic mixing rule. For mixtures (vapor or liquid)
The first approach is to use the same equation developed for with composition x i and total of N components the following
pure substances but the input parameters (T c , P c , and ω) are equations are used to calculate a and b for various types of
estimated for the mixture. Estimation of these pseudocritical cubic EOS:
properties for petroleum fractions and defined hydrocarbon N
N

mixtures were discussed in Chapter 3. The second approach (5.59) a mix = x i x j a ij
is to estimate desired physical property (i.e., molar volume i=1 j=1
or density) for all pure compounds using the above equations N

and then to calculate the mixture property using the mixture (5.60) b mix = x i b i
composition through an appropriate mixing rule for the prop- i=1
erty (i.e., Eq. (3.44) for density). This approach in some cases where a ij is given by the following equation:
gives good estimate of the property but requires large calcu- 1/2
lation time especially for mixtures containing many compo- (5.61) a ij = (a i a j ) (1 − k ij )
nents. The third and most widely used approach is to calculate For the volume translation c, the mixing rule is the same as
EOS parameters (parameters a and b) for the mixture using for parameter b:
their values for pure components and mixture composition. N
The simplest EOS for gases is the ideal gas law given by Eq. (5.62)
(5.14). When this is applied to component i with n i moles in c mix = i=1 x i c i
a mixture we have
In Eq. (5.61), k ij is a dimensionless parameter called binary in-
t
(5.56) PV = n i RT teraction parameter (BIP), where k ii = 0 and k ij = k ji . For most
i

--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---

Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT