Page 232 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

T1: IML
QC: IML/FFX
P1: IML/FFX
P2: IML/FFX
17:42
August 16, 2007
AT029-Manual
AT029-05
AT029-Manual-v7.cls
212 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
3
where V c is the molar critical volume in cm /mol and d is
50
a parameter that is determined for several compounds, i.e.,
d = 0.6 for methane, 1 for ethane, 1.8 for neopentane, 2.5 for
Second Virial Coeffecient, B, cm 3 /mole -150 McGlashan practical and generalized correlation for third virial coeffi-
-50
benzene, and 4.25 for n-octane. In general when T r > 1.5 the
second term in the above equation is insignificant. A more
cient was proposed by Orbey and Vera [44] for nonpolar com-
pounds in a form similar to Eq. (5.71), which was proposed
for the second virial coefficients:
-250
Normal Fluids
2
Tsonopoulos
CP
(0)
(1)
c
= C
+ ωC
Experimental Data
2
(RT c)
-350
0.02432
(0)
C
(5.78)
= 0.01407 +
T r 2.8 − 0.00313
10.5
T
r
-450
0.0177 0.040 0.003 0.00228
100 300 500 700 900 1100 C (1) =−0.02676 + + − −
T 2.8 T 3 T 6 T 10.5
Temperature, K r r r r
where C (0) and C (1) are dimensionless parameters for simple
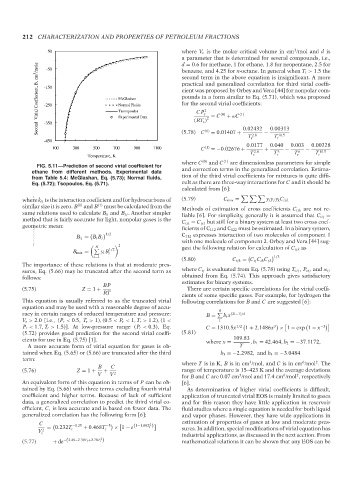
FIG. 5.11—Prediction of second virial coefficient for
ethane from different methods. Experimental data and correction terms in the generalized correlation. Estima-
from Table 5.4: McGlashan, Eq. (5.73); Normal fluids, tion of the third virial coefficients for mixtures is quite diffi-
Eq. (5.72); Tsopoulos, Eq. (5.71). cult as there are three-way interactions for C and it should be
calculated from [6]:

where k ij is the interaction coefficient and for hydrocarbons of (5.79) C mix = y i y j y k C ijk
similar size it is zero. B (0) and B (1) must be calculated from the Methods of estimation of cross coefficients C ijk are not re-
same relations used to calculate B ii and B jj . Another simpler
liable [6]. For simplicity, generally it is assumed that C iij =
method that is fairly accurate for light, nonpolar gases is the C iji = C jii but still for a binary system at least two cross coef-
geometric mean:
ficients of C 112 and C 122 must be estimated. In a binary system,
1/2
C 112 expresses interaction of two molecules of component 1
B ij = B i B j
with one molecule of component 2. Orbey and Vera [44] sug-
2
N ! gest the following relation for calculation of C ijk as
--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
B mix = y i B i 1/2
i=1 1/3
(5.80) C ijk = C ij C ik C jk
The importance of these relations is that at moderate pres-
sures, Eq. (5.66) may be truncated after the second term as where C ij is evaluated from Eq. (5.78) using T cij , P cij and ω ij
follows: obtained from Eq. (5.74). This approach gives satisfactory
BP estimates for binary systems.
(5.75) Z = 1 + There are certain specific correlations for the virial coeffi-
RT cients of some specific gases. For example, for hydrogen the
This equation is usually referred to as the truncated virial following correlations for B and C are suggested [6]:
equation and may be used with a reasonable degree of accu-
racy in certain ranges of reduced temperature and pressure: 4 ! (2i−1)/4
B = b i x
V r > 2.0 [i.e., (P r < 0.5, T r > 1), (0.5 < P r < 1, T r > 1.2), (1 < 1
P r < 1.7, T r > 1.5)]. At low-pressure range (P r < 0.3), Eq. C = 1310.5x 1/2 1 + 2.1486x 3 × 1 − exp 1 − x −3

(5.72) provides good prediction for the second virial coeffi- (5.81)
cients for use in Eq. (5.75) [1]. where x = 109.83 , b 1 = 42.464, b 2 =−37.1172,
A more accurate form of virial equation for gases is ob- T
tained when Eq. (5.65) or (5.66) are truncated after the third b 3 =−2.2982, and b 4 =−3.0484
term: 3 6 2
B C where T is in K, B is in cm /mol, and C is in cm /mol . The
(5.76) Z = 1 + + range of temperature is 15–423 K and the average deviations
V V 2 for B and C are 0.07 cm /mol and 17.4 cm /mol , respectively
2
3
6
An equivalent form of this equation in terms of P can be ob- [6].
tained by Eq. (5.66) with three terms excluding fourth virial As determination of higher virial coefficients is difficult,
coefficient and higher terms. Because of lack of sufficient application of truncated virial EOS is mainly limited to gases
data, a generalized correlation to predict the third virial co- and for this reason they have little application in reservoir
efficient, C, is less accurate and is based on fewer data. The fluid studies where a single equation is needed for both liquid
generalized correlation has the following form [6]: and vapor phases. However, they have wide applications in
C −0.25 −5 ( 1−1.89T r ) estimation of properties of gases at low and moderate pres-
2
= 0.232T + 0.468T × 1 − e sures. In addition, special modifications of virial equation has
V c 2 r r
industrial applications, as discussed in the next section. From
2
(5.77) + de −( 2.49−2.30T r +2.70T r ) mathematical relations it can be shown that any EOS can be
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT