Page 246 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P2: IML/FFX
T1: IML
P1: IML/FFX
QC: IML/FFX
August 16, 2007
AT029-Manual-v7.cls
AT029-Manual
AT029-05
17:42
226 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
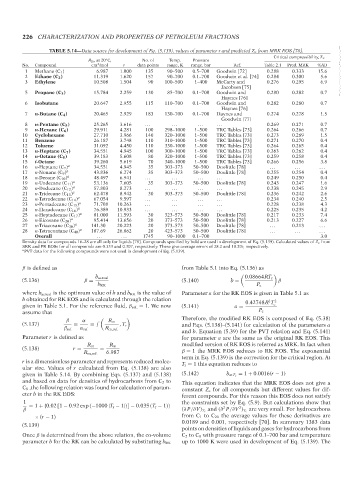
TABLE 5.14—Data source for development of Eq. (5.139), values of parameter r and predicted Z c from MRK EOS [70].
Critical compressibility, Z c
R m ,at20 C, No. of Temp. Pressure
◦
3
No. Compound cm /mol r data points range, K range, bar Ref. Table 2.1 Pred. MRK %AD
1 Methane (C 1 ) 6.987 1.000 135 90–500 0.5–700 Goodwin [72] 0.288 0.333 15.6 --`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
2 Ethane (C 2 ) 11.319 1.620 157 90–700 0.1–700 Goodwin et al. [74] 0.284 0.300 5.6
3 Ethylene 10.508 1.504 90 100–500 1–400 McCarty and 0.276 0.295 6.9
Jacobsen [75]
5 Propane (C 3 ) 15.784 2.259 130 85–700 0.1–700 Goodwin and 0.280 0.282 0.7
Haynes [76]
6 Isobutane 20.647 2.955 115 110–700 0.1–700 Goodwin and 0.282 0.280 0.7
Haynes [76]
7 n-Butane (C 4 ) 20.465 2.929 183 130–700 0.1–700 Haynes and 0.274 0.278 1.5
Goodwin [77]
8 n-Pentane (C 5 ) 25.265 3.616 . . . . . . . . . . . . 0.269 0.271 0.7
9 n-Hexane (C 6 ) 29.911 4.281 100 298–1000 1–500 TRC Tables [73] 0.264 0.266 0.7
10 Cyclohexane 27.710 3.966 140 320–1000 1–500 TRC Tables [73] 0.273 0.269 1.5
11 Benzene 26.187 3.748 110 310–1000 1–500 TRC Tables [73] 0.271 0.270 0.4
12 Toluene 31.092 4.450 110 330–1000 1–500 TRC Tables [73] 0.264 0.265 0.4
13 n-Heptane (C 7 ) 34.551 4.945 100 300–1000 1–500 TRC Tables [73] 0.263 0.262 0.4
14 n-Octane (C 8 ) 39.183 5.608 80 320–1000 1–500 TRC Tables [73] 0.259 0.258 0.4
15 i-Octane 39.260 5.619 70 340–1000 1–500 TRC Tables [73] 0.266 0.256 3.8
16 n-Heptane (C 7 ) a 34.551 4.945 35 303–373 50–500 Doolittle [78] . . . . . . . . .
17 n-Nonane (C 9 ) a 43.836 6.274 35 303–373 50–500 Doolittle [78] 0.255 0.254 0.4
18 n-Decane (C 10 ) a 48.497 6.941 . . . . . . . . . . . . 0.249 0.250 0.4
19 n-Undecane (C 11 ) a 53.136 7.605 35 303–373 50–500 Doolittle [78] 0.243 0.247 1.6
20 n-Dodecane (C 12 ) a 57.803 8.273 . . . . . . . . . . . . 0.238 0.245 2.9
21 n-Tridecane (C 13 ) a 62.478 8.942 30 303–373 50–500 Doolittle [78] 0.236 0.242 2.6
22 n-Tetradecane (C 14 ) a 67.054 9.597 . . . . . . . . . . . . 0.234 0.240 2.5
23 n-Pentadecane (C 15 ) a 71.708 10.263 . . . . . . . . . . . . 0.228 0.238 4.3
24 n-Hexadecane (C 16 ) a 76.389 10.933 . . . . . . . . . . . . 0.225 0.235 4.2
25 n-Heptadecane (C 17 ) a 81.000 11.593 30 323–573 50–500 Doolittle [78] 0.217 0.233 7.4
26 n-Eicosane (C 20 ) a 95.414 13.656 20 373–573 50–500 Doolittle [78] 0.213 0.227 6.6
27 n-Triacosane (C 30 ) a 141.30 20.223 20 373–573 50–500 Doolittle [78] . . . 0.213 . . .
28 n-Tetracontane (C 40 ) a 187.69 26.862 20 423–573 50–500 Doolittle [78] . . . . . . . . .
Overall . . . . . . 1745 90–1000 0.1–700 3.0
Density data for compounds 16–28 are all only for liquids [78]. Compounds specified by bold are used in development of Eq. (5.139). Calculated values of Z c from
SRK and PR EOSs for all compounds are 0.333 and 0.307, respectively. These give average errors of 28.2 and 18.2%, respectively.
a PVT data for the following compounds were not used in development of Eq. (5.139).
β is defined as from Table 5.1 into Eq. (5.136) as

b actual 0.08664RT c
(5.136) β = (5.140) b = β
b RK P c
where b actual is the optimum value of b and b RK is the value of Parameter a for the RK EOS is given in Table 5.1 as
b obtained for RK EOS and is calculated through the relation 0.42748R T 2
2
given in Table 5.1. For the reference fluid, β ref. = 1. We now (5.141) a = c
assume that P c
Therefore, the modified RK EOS is composed of Eq. (5.38)
β α R m

(5.137) = = f , T r and Eqs. (5.138)–(5.141) for calculation of the parameters a
β ref α ref R m,ref.
and b. Equation (5.39) for the PVT relation and Eq. (5.141)
Parameter r is defined as for parameter a are the same as the original RK EOS. This
modified version of RK EOS is referred as MRK. In fact when
R m R m
(5.138) r = = β = 1 the MRK EOS reduces to RK EOS. The exponential
R m,ref. 6.987
term in Eq. (5.139) is the correction for the critical region. At
r is a dimensionless parameter and represents reduced molec- T r = 1 this equation reduces to
ular size. Values of r calculated from Eq. (5.138) are also
given in Table 5.14. By combining Eqs. (5.137) and (5.138) (5.142) b at T c = 1 + 0.0016(r − 1)
and based on data for densities of hydrocarbons from C 2 to This equation indicates that the MRK EOS does not give a
C 8 ,the following relation was found for calculation of param- constant Z c for all compounds but different values for dif-
eter b in the RK EOS: ferent compounds. For this reason this EOS does not satisfy
1 the constraints set by Eq. (5.9). But calculations show that
= 1 + {0.02 [1 − 0.92 exp (−1000 |T r − 1|)] − 0.035 (T r − 1)} 2 2
β (∂ P/∂V) T c and (∂ P/∂V ) T c are very small. For hydrocarbons
× (r − 1) from C 1 to C 20 the average values for these derivatives are
0.0189 and 0.001, respectively [70]. In summary 1383 data
(5.139)
points on densities of liquids and gases for hydrocarbons from
Once β is determined from the above relation, the co-volume C 2 to C 8 with pressure range of 0.1–700 bar and temperature
up to 1000 K were used in development of Eq. (5.139). The
parameter b for the RK can be calculated by substituting b RK

Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT