Page 352 - Mechanical Behavior of Materials

Section 8.4 Application of K to Design and Analysis 353

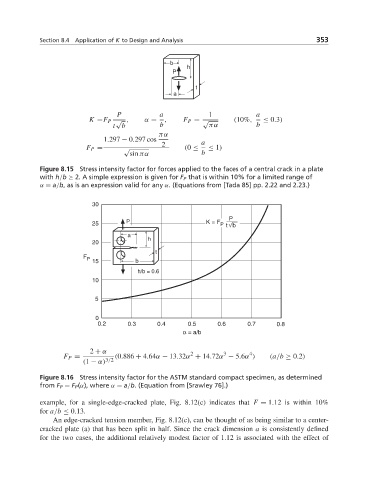
b
h
P
t
a

P a 1 a
K =F P √ , α = , F P = √ (10%, ≤ 0.3)
t b b πα b
πα
1.297 − 0.297 cos
2 a
F P = √ (0 ≤ ≤ 1)
sin πα b
Figure 8.15 Stress intensity factor for forces applied to the faces of a central crack in a plate
with h/b ≥ 2. A simple expression is given for F P that is within 10% for a limited range of
α = a/b, as is an expression valid for any α. (Equations from [Tada 85] pp. 2.22 and 2.23.)

30

P
25 P K = F P t b
a
h
20
t
F
P
15 b
h/b = 0.6
10

5

0
0.2 0.3 0.4 0.5 0.6 0.7 0.8
α = a/b

2 + α 2 3 4
F P = (0.886 + 4.64α − 13.32α + 14.72α − 5.6α ) (a/b ≥ 0.2)
(1 − α) 3/2
Figure 8.16 Stress intensity factor for the ASTM standard compact specimen, as determined
from F P = F P (α), where α = a/b. (Equation from [Srawley 76].)

example, for a single-edge-cracked plate, Fig. 8.12(c) indicates that F = 1.12 is within 10%
for a/b ≤ 0.13.
An edge-cracked tension member, Fig. 8.12(c), can be thought of as being similar to a center-
cracked plate (a) that has been split in half. Since the crack dimension a is consistently defined
for the two cases, the additional relatively modest factor of 1.12 is associated with the effect of