Page 88 -

72 2. Boundary Integral Equations

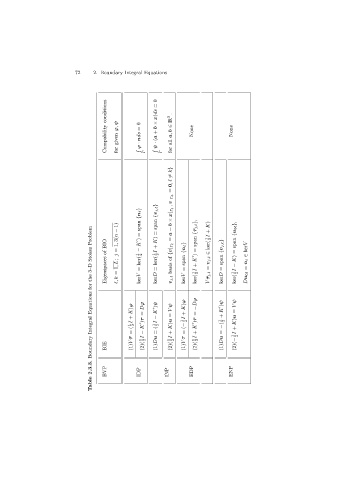
conditions =0 x)ds × . IR 3

Compability ϕ, ψ given for =0 nds · ϕ Γ b + (a · ψ Γ ∈ a, b all for None None

k}
=
0,
=
, v| Γ k

{n } {v j, } x| Γ

1) span span × b + {τ j, }, K) {u 0 },
Problem BIO − 1, 3(n = K ) = K) a = span + ker( 1 I 2 span

Stokes of = j − 2 + =ker( 1 I 2 {v| Γ of {n } span = K ) ∈ v j, {v j, } span = K) kerV ∈

3–D Eigenspaces 1,L ; =ker( 1 basis = + = = − n =
the = , k kerV kerD v j, kerV ker( 1 I 2 τ j, V kerD ker( 1 I 2 Du 0
for
Equations K)ϕ Dϕ = K )ψ ψ V K)ϕ + −Dϕ = K )ψ ψ V =

Integral + =( 1 I 2 K )τ − − =( 1 I 2 = K)u + =(− 1 I 2 K )τ + + −( 1 = 2 K)u + 2

Boundary BIE τ (1)V (2)( 1 I 2 (1)Du (2)( 1 I 2 τ (1)V (2)( 1 I 2 (1)Du (2)(− 1 I

2.3.3. BVP IDP INP EDP ENP

Table