Page 326 - Introduction to Statistical Pattern Recognition

308 Introduction to Statistical Pattern Recognition

0.5

0.4

0.3
3
.-r
L
0.2

I
0.

0
0 0.05 0.10 0.15 0.20 0.25
500 = ql(x)q*oo
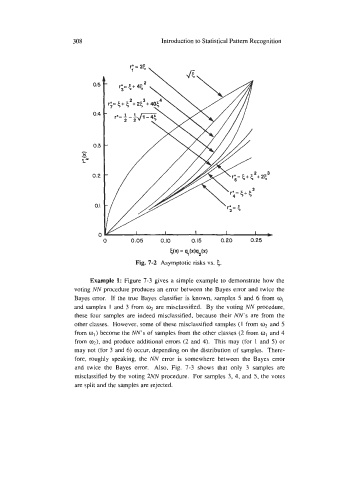
Fig. 7-2 Asymptotic risks vs. 5.

Example 1: Figure 7-3 gives a simple example to demonstrate how the
voting NN procedure produces an error between the Bayes error and twice the
Bayes error. If the true Bayes classifier is known, samples 5 and 6 from wI
and samples 1 and 3 from o2 are misclassified. By the voting NN procedure,
these four samples are indeed misclassified, because their NN’s are from the
other classes. However, some of these misclassified samples (1 from w2 and 5
from 01) become the NN’s of samples from the other classes (2 from wI and 4
from a*), and produce additional errors (2 and 4). This may (for 1 and 5) or
may not (for 3 and 6) occur, depending on the distribution of samples. There-
fore, roughly speaking, the NN error is somewhere between the Bayes error
and twice the Bayes error. Also, Fig. 7-3 shows that only 3 samples are
misclassified by the voting 2NN procedure. For samples 3, 4, and 5, the votes
are split and the samples are rejected.