Page 295 - Materials Chemistry, Second Edition

11 Uncertainty Management and Sensitivity Analysis 281

decision, choosing midpoint indicators because they can be quantified with higher
precision will still not avoid the uncertainty of that decision’s environmental con-
sequences since a midpoint indicator is less relevant (representative) for the envi-
ronmental consequences to be avoided. Weidema (2009) entertainingly compares
this flawed logic as being “representative of the situation of the drunk who, when
asked why he was searching for his keys under the streetlight although he had lost
them in the dark alley, responded that it was easier to see under the light”.In
consequence, the overall uncertainty of endpoint indicators may not (always) be
much different to that of midpoint indicators from a decision-support perspective as
indicated in Fig. 11.4 where the development in the “overall uncertainty” accom-
panying the decision may sometimes be lowest at the damage level, when the
reduction in interpretation uncertainty, going from midpoint to damage, more than
compensates the increase in model and parameter uncertainty of the applied char-
acterisation model.
Hopefully, these examples illustrate that when discussing uncertainties between
LCA indicators (of different impact categories or between midpoint and endpoint
level), all types of uncertainty combined with the related concepts of precision and
accuracy need to be considered or else the risk of oversimplifying and comparing
apples and oranges is imminent, which may lead to unjustified and wrong
conclusions.
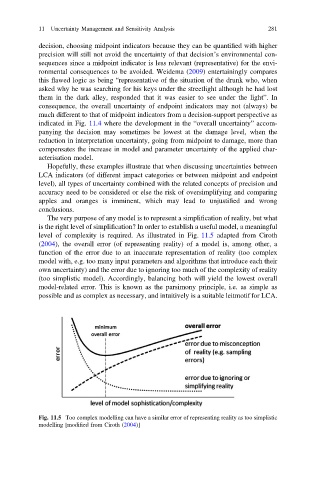
The very purpose of any model is to represent a simplification of reality, but what
is the right level of simplification? In order to establish a useful model, a meaningful
level of complexity is required. As illustrated in Fig. 11.5 adapted from Ciroth
(2004), the overall error (of representing reality) of a model is, among other, a
function of the error due to an inaccurate representation of reality (too complex
model with, e.g. too many input parameters and algorithms that introduce each their
own uncertainty) and the error due to ignoring too much of the complexity of reality
(too simplistic model). Accordingly, balancing both will yield the lowest overall
model-related error. This is known as the parsimony principle, i.e. as simple as
possible and as complex as necessary, and intuitively is a suitable leitmotif for LCA.

Fig. 11.5 Too complex modelling can have a similar error of representing reality as too simplistic
modelling [modified from Ciroth (2004)]