Page 300 - A First Course In Stochastic Models

294 SEMI-MARKOV DECISION PROCESSES

Numerical results
We consider the switching cost function K(a, b) = κ |a − b| and assume the numer-
ical data
s = 10, µ = 1, r = 30 and h = 10.

The arrival rate λ is 7 and 8, while the proportionality constant κ for the switching
cost has the two values 10 and 25. In each example, we take the bound M = 20 for
the states (i, t) with i ≥ M in which all of the s channels are always turned on. The
value-iteration algorithm is started with V 0 ((i, t)) = 0 for all states (i, t) and uses
the tolerance number ε = 10 −3 for its stopping criterion. Our numerical calculations
indicate that for the case of linear switching costs, the average cost optimal control
rule is characterized by parameters s(i) and t(i): the number of channels turned on
is raised up to the level s(i) in the states (i, t) with t < s(i), the number of channels
turned on is left unchanged in the states (i, t) with s(i) ≤ t ≤ t(i) and the number
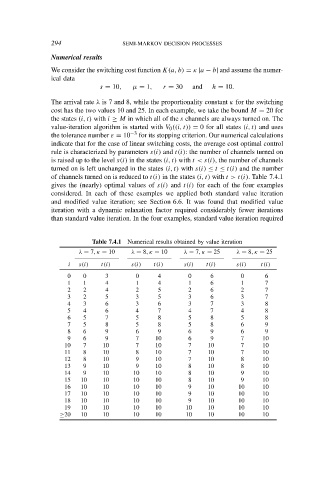
of channels turned on is reduced to t(i) in the states (i, t) with t > t(i). Table 7.4.1
gives the (nearly) optimal values of s(i) and t(i) for each of the four examples
considered. In each of these examples we applied both standard value iteration
and modified value iteration; see Section 6.6. It was found that modified value
iteration with a dynamic relaxation factor required considerably fewer iterations
than standard value iteration. In the four examples, standard value iteration required

Table 7.4.1 Numerical results obtained by value iteration
λ = 7, κ = 10 λ = 8, κ = 10 λ = 7, κ = 25 λ = 8, κ = 25
i s(i) t(i) s(i) t(i) s(i) t(i) s(i) t(i)
0 0 3 0 4 0 6 0 6
1 1 4 1 4 1 6 1 7
2 2 4 2 5 2 6 2 7
3 2 5 3 5 3 6 3 7
4 3 6 3 6 3 7 3 8
5 4 6 4 7 4 7 4 8
6 5 7 5 8 5 8 5 8
7 5 8 5 8 5 8 6 9
8 6 9 6 9 6 9 6 9
9 6 9 7 10 6 9 7 10
10 7 10 7 10 7 10 7 10
11 8 10 8 10 7 10 7 10
12 8 10 9 10 7 10 8 10
13 9 10 9 10 8 10 8 10
14 9 10 10 10 8 10 9 10
15 10 10 10 10 8 10 9 10
16 10 10 10 10 9 10 10 10
17 10 10 10 10 9 10 10 10
18 10 10 10 10 9 10 10 10
19 10 10 10 10 10 10 10 10
≥20 10 10 10 10 10 10 10 10