Page 266 - Acquisition and Processing of Marine Seismic Data

5.5 BAND-PASS FILTER 257

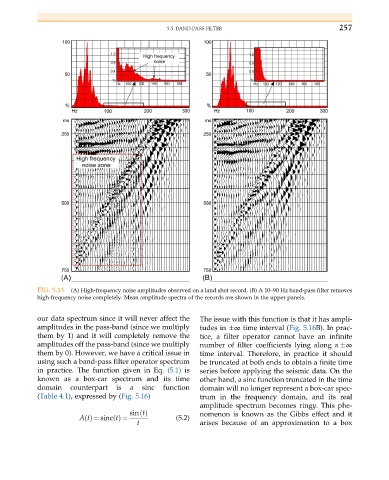
FIG. 5.15 (A) High-frequency noise amplitudes observed on a land shot record. (B) A 10–90 Hz band-pass filter removes
high-frequency noise completely. Mean amplitude spectra of the records are shown in the upper panels.

our data spectrum since it will never affect the The issue with this function is that it has ampli-
amplitudes in the pass-band (since we multiply tudes in ∞ time interval (Fig. 5.16B). In prac-
them by 1) and it will completely remove the tice, a filter operator cannot have an infinite
amplitudes off the pass-band (since we multiply number of filter coefficients lying along a ∞
them by 0). However, we have a critical issue in time interval. Therefore, in practice it should
using such a band-pass filter operator spectrum be truncated at both ends to obtain a finite time
in practice. The function given in Eq. (5.1) is series before applying the seismic data. On the
known as a box-car spectrum and its time other hand, a sinc function truncated in the time
domain counterpart is a sinc function domain will no longer represent a box-car spec-
(Table 4.1), expressed by (Fig. 5.16) trum in the frequency domain, and its real
amplitude spectrum becomes ringy. This phe-
sin tðÞ nomenon is known as the Gibbs effect and it
AtðÞ ¼ sinc tðÞ ¼ (5.2)
t arises because of an approximation to a box