Page 512 - Acquisition and Processing of Marine Seismic Data

11.2 KIRCHHOFF MIGRATION 503

migration aperture, which directly controls the hyperbolas theoretically extend to infinite time
quality and accuracy of the migrated output as lengths and distances. Since it is impossible to
well as the run time of the diffraction summa- work on such infinite theoretical hyperbolas,
tion algorithm. Although Kirchhoff migration they are truncated in the space dimension in
can handle steep dips up to 90 degrees, it is also practice. The spatial extent of the diffraction
possible to restrict the algorithm by means of the hyperbola that the actual summation path spans
maximum structural dip to migrate, which may is termed the migration aperture or the aperture
reduce the computational cost. Kirchhoff migra- width, and is defined as the number of traces
tion is sensitive to velocity errors and the veloc- involved in the computation or the maximum
ity analysis must be performed carefully to horizontal distance that the diffraction hyper-
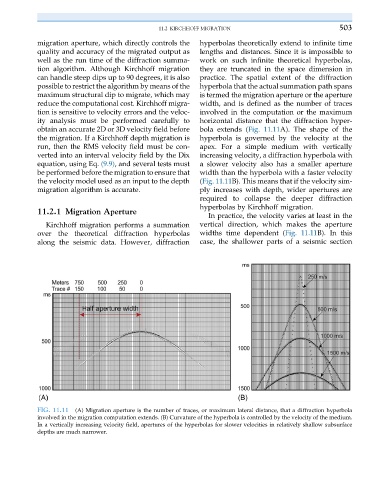
obtain an accurate 2D or 3D velocity field before bola extends (Fig. 11.11A). The shape of the
the migration. If a Kirchhoff depth migration is hyperbola is governed by the velocity at the
run, then the RMS velocity field must be con- apex. For a simple medium with vertically
verted into an interval velocity field by the Dix increasing velocity, a diffraction hyperbola with
equation, using Eq. (9.9), and several tests must a slower velocity also has a smaller aperture
be performed before the migration to ensure that width than the hyperbola with a faster velocity
the velocity model used as an input to the depth (Fig. 11.11B). This means that if the velocity sim-
migration algorithm is accurate. ply increases with depth, wider apertures are
required to collapse the deeper diffraction
hyperbolas by Kirchhoff migration.
11.2.1 Migration Aperture
In practice, the velocity varies at least in the
Kirchhoff migration performs a summation vertical direction, which makes the aperture
over the theoretical diffraction hyperbolas widths time dependent (Fig. 11.11B). In this
along the seismic data. However, diffraction case, the shallower parts of a seismic section

FIG. 11.11 (A) Migration aperture is the number of traces, or maximum lateral distance, that a diffraction hyperbola
involved in the migration computation extends. (B) Curvature of the hyperbola is controlled by the velocity of the medium.
In a vertically increasing velocity field, apertures of the hyperbolas for slower velocities in relatively shallow subsurface
depths are much narrower.