Page 522 - Acquisition and Processing of Marine Seismic Data

11.4 FREQUENCY-WAVENUMBER (f-k) MIGRATION 513

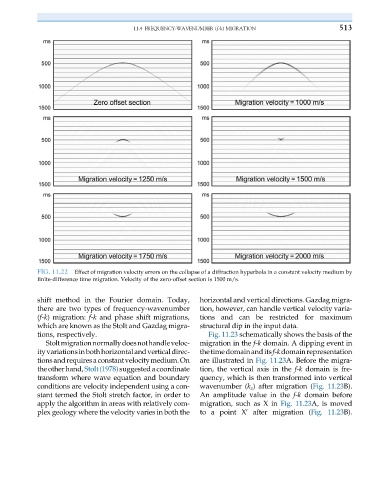
FIG. 11.22 Effect of migration velocity errors on the collapse of a diffraction hyperbola in a constant velocity medium by
finite-difference time migration. Velocity of the zero-offset section is 1500 m/s.

shift method in the Fourier domain. Today, horizontal and vertical directions. Gazdag migra-
there are two types of frequency-wavenumber tion, however, can handle vertical velocity varia-
(f-k) migration: f-k and phase shift migrations, tions and can be restricted for maximum
which are known as the Stolt and Gazdag migra- structural dip in the input data.
tions, respectively. Fig. 11.23 schematically shows the basis of the
Stoltmigrationnormallydoesnothandleveloc- migration in the f-k domain. A dipping event in
ityvariationsinbothhorizontalandverticaldirec- thetimedomainanditsf-kdomainrepresentation
tionsandrequiresaconstantvelocitymedium.On are illustrated in Fig. 11.23A. Before the migra-
theotherhand,Stolt(1978)suggestedacoordinate tion, the vertical axis in the f-k domain is fre-
transform where wave equation and boundary quency, which is then transformed into vertical
conditions are velocity independent using a con- wavenumber (k z ) after migration (Fig. 11.23B).
stant termed the Stolt stretch factor, in order to An amplitude value in the f-k domain before
apply the algorithm in areas with relatively com- migration, such as X in Fig. 11.23A, is moved
0
plex geology where the velocity varies in both the to a point X after migration (Fig. 11.23B).