Page 523 - Acquisition and Processing of Marine Seismic Data

514 11. SEISMIC MIGRATION

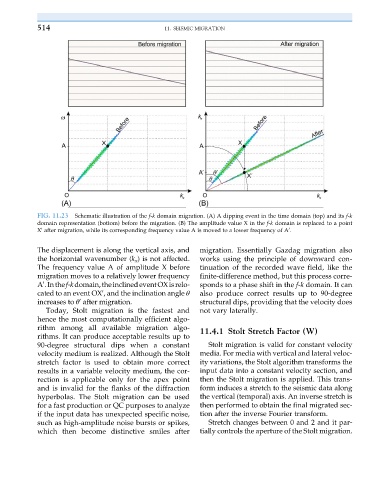
FIG. 11.23 Schematic illustration of the f-k domain migration. (A) A dipping event in the time domain (top) and its f-k
domain representation (bottom) before the migration. (B) The amplitude value X in the f-k domain is replaced to a point
0
X after migration, while its corresponding frequency value A is moved to a lower frequency of A . 0
The displacement is along the vertical axis, and migration. Essentially Gazdag migration also
the horizontal wavenumber (k x ) is not affected. works using the principle of downward con-
The frequency value A of amplitude X before tinuation of the recorded wave field, like the
migration moves to a relatively lower frequency finite-difference method, but this process corre-
A .Inthef-kdomain,theinclinedeventOXisrelo- sponds to a phase shift in the f-k domain. It can
0
cated to an event OX , and the inclination angle θ also produce correct results up to 90-degree
0
increases to θ after migration. structural dips, providing that the velocity does
0
Today, Stolt migration is the fastest and not vary laterally.
hence the most computationally efficient algo-
rithm among all available migration algo- 11.4.1 Stolt Stretch Factor (W)
rithms. It can produce acceptable results up to
90-degree structural dips when a constant Stolt migration is valid for constant velocity
velocity medium is realized. Although the Stolt media. For media with vertical and lateral veloc-
stretch factor is used to obtain more correct ity variations, the Stolt algorithm transforms the
results in a variable velocity medium, the cor- input data into a constant velocity section, and
rection is applicable only for the apex point then the Stolt migration is applied. This trans-
and is invalid for the flanks of the diffraction form induces a stretch to the seismic data along
hyperbolas. The Stolt migration can be used the vertical (temporal) axis. An inverse stretch is
for a fast production or QC purposes to analyze then performed to obtain the final migrated sec-
if the input data has unexpected specific noise, tion after the inverse Fourier transform.
such as high-amplitude noise bursts or spikes, Stretch changes between 0 and 2 and it par-
which then become distinctive smiles after tially controls the aperture of the Stolt migration.